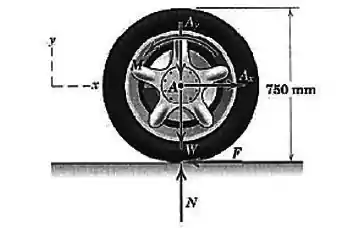
A roda traseira de um automóvel de tração dianteira que está acelerando para a direita está submetida às cinco forças e ao momento mostrado. As forças e são forças transmitidas pelo eixo à roda, é a força de fricção exercida pela superfície da estrada no pneu, éa força normal de reação exercida pela superfície da estrada e é o peso do conjunto pneu/roda. O momento é devido à fricção do mancal. Determine e localize a resultante do sistema.
Passo 1
Primeiro vamos calcular a resultante das forças. Para isso, vamos antes escrever cada força em termos de e (veja na figura as forças que são totalmente verticais ou horizontais):
Passo 2
Assim, a resultante é dada por:
Ou seja, a nossa resultante é totalmente horizontal. Vamos agora calcular o momento resultante total do sistema e depois a localização da resultante das forças.
Passo 3
Vamos calcular o momento total em relação ao ponto .
Isso vai nos ajudar porque apenas a força exerce momento nesse ponto. Veja na figura: As outras forças têm linhas de ação que cruzam com
Assim, o sistema pode ser simplificado para:
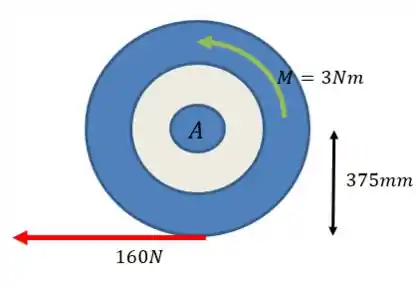
Tomando o sentido horário como positivo, teremos:
Passo 4
Show de bola. Agora só precisamos descobrir a localização da resultante.
Podemos tirar uma informação importante do nosso momento resultante e do sentido da força resultante.
O momento resultante é no sentido horário e a força resultante aponta no sentido positivo de . Assim, considerando como referência, a força resultante vai estar localizada acima desse ponto:
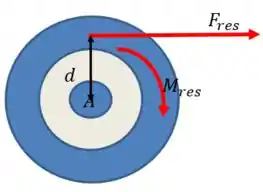
Pra descobrir quanto vale , basta usarmos:
Então, a resultante está acima do ponto .
Resposta
A resultante está acima do ponto .