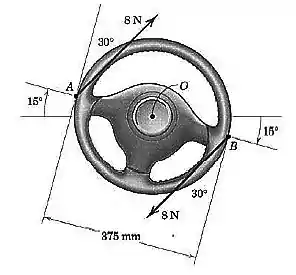
Durante uma curva suave para a direita, uma pessoa exerce as forças mostradas sobre o volante. Observe que cada força consiste em uma componente tangencial e em uma componente radial direcionada para dentro. Determine o momento exercido em relação à coluna de volante
Passo 1
Nós apenas precisamos lidar com o ângulo de , afinal de contas, ele é o ângulo que a força faz com a tangente ao círculo. A partir dele, vamos decompor a força em um vetor na direção do raio (radial) e que não realiza momento, e uma componente tangencial que realiza o momento.
Passo 2
A linha pontilhada representa a direção tangencial ao círculo:

Assim, podemos perceber que a componente tangencial é dada por:
E a radial:
A componente na direção radial não realiza momento, então:
Perceba que somamos os momentos das duas forças, pois eles tem o mesmo sinal.
Então: