Considere uma amostra de tempos de falha de um componente elétrico (meses) que tenha gerado o seguinte boxplot:
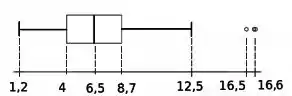
c) Encarando agora esse boxplot como se ele fosse uma distribuição de probabilidade, ou seja, encarando os quartis amostrais como se fossem quartis populacionais, suponha que componentes sejam sorteados (com reposição e de modo independente) e que se anote o tempo que levou até o componente falhar. Usando o TCL, obtenha uma aproximação para a probabilidade de observarmos mais de componentes cujos tempos de falha tenham sido menores que meses.
Passo 1
(c)
Queremos a prob. de componentes, dentre os , falharem antes de meses.
Primeiro vamos pensar em qual seria a prob. de um componente qualquer falhar antes de meses.
Esse é o nosso terceiro quartil, certo? O ... isso significa que dos valores estão abaixo dele, ou seja, de chance de um componente aleatório falhar antes de meses.
Passo 2
Agora que a gente já sabe a prob. de sucesso pra um componente qualquer (que é a prob. de falhar antes de meses), vamos avançar:
Se cada componente é retirado com reposição, de forma independente e todos tem a mesma prob. de falharem antes do tempo determinado... então estamos tratando de uma Binomial.
E temos que calcular a prob. de mais de falharem...
Passo 3
Rapaz, mas é muito grande, concorda? Lembra o que a gente faz quando isso acontece? O enunciado deu até a dica pra gente...
Podemos usar o Teorema Central do Limite e aproximar a Binomial por uma Normal com:
E:
Daí:
Passo 4
E com isso calculamos pela normal... (usando a correção de continuidade).
Usando a tabela da Normal: