Os quadros abaixo correspondem as alturas dos alunos matriculados na disciplina PROBEST-2012-2. Construa o boxplot determinando se há valores discrepantes no conjunto de dados apresentados.
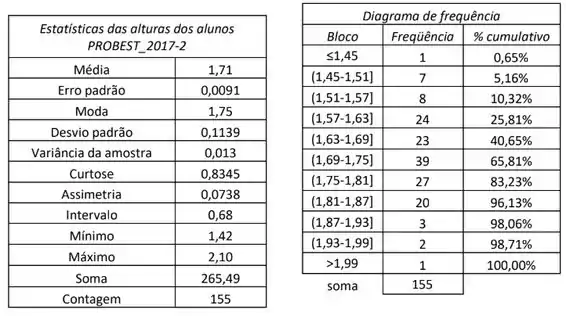
Passo 1
Fala galerinha, beleza? Partiu mais uma questão de probabilidade?
Nesse problema vamos ter que montar o Boxplot do conjunto de dados fornecido para gente. Para isso, vamos lembrar um pouco o que é isso:
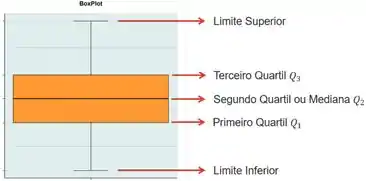
Num boxplot, devemos informar os três quartis de uma distribuição e seus limites inferior e superior. Vou explicar com bastante calma como obter essas coisas nos próximos passos!
Passo 2
Os quartis são valores que dividem a distribuição em quatro partes iguais. Por exemplo, vamos considerar a seguinte distribuição em ordem crescente:
Podemos dividir essa amostra de números em quatro partes com números cada uma:
O primeiro quartil é um número que separa a parte 1 da parte 2. Nesse caso podemos tomar . O segundo quartil é um número que divide a amostra no meio (é exatamente a mediana), nesse caso . Já o terceiro quartil divide a parte 3 da 4: .
Agora vamos ao nosso problema! Para achar os quartis precisamos olhar para a tabela de frequência. Para qual intervalo a porcentagem acumulada é ?
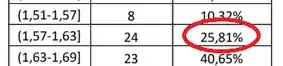
Isso ocorre no intervalo . Isso significa que que para algum dos 24 valores nesse intervalo atingimos a fronteira dos . Esse valor será o primeiro quartil. Mas temos um problema: não conhecemos cada um desses valores, de modo que não podemos achar com certeza quem é o primeiro quartil. Por isso, vamos fazer uma estimativa (e aqui não existe resposta única)!
O maior valor nesse intervalo (que deve estar bem próximo de ) corresponde a da porcentagem acumulada. Isso significa que o primeiro quartil deve estar bem mais próximo de do que de . Portanto, vou chutar algo próximo de :
Para o segundo quartil temos que olhar para o intervalo em que a porcentagem acumulada ultrapassa os :
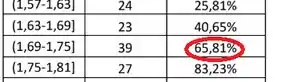
Vemos que ele deve estar entre e . Além disso, ele deve estar mais próximo de do que de . Vou chutar algo perto de :
Para o terceiro quartil, olhamos para o intervalo em que passamos dos :
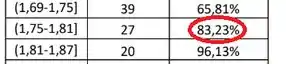
Vemos que ele está no intervalo . Ele deve estar mais próximo de do que de , porém bem próximo do meio do intervalo também. Com isso, vou chutar algo perto de :
Com isso nós já temos os três quartis:
Passo 3
O próximo passo é encontrar os limites inferior e superior. Aí você precisa lembrar que eles são definidos por
Vamos olhar primeiro para o limite inferior:
Na primeira tabela, foi dado que o mínimo dos dados é :
Para o limite superior, temos
O valor máximo dos dados (primeira tabela) é :
Com isso podemos fazer nosso boxplot!
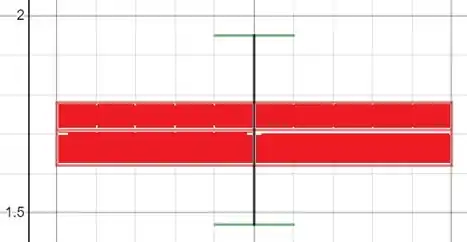
Passo 4
O último passo é verificar se existem valores discrepantes. Esses são valores que estariam fora dos limites inferior e superior, ou seja, valores que
Vimos que o valor máximo da distribuição é e o mínimo é . É evidente que esses valores estão foram dessa região! Portanto, esse conjunto de dados apresenta sim valores discrepantes!
Resposta
Esboço de gráfico.