As tabelas na parte inferior correspondem às alturas dos alunos matriculados na disciplina PROBEST-2013-2, turma 3VB. Usando os dados apresentados, pede-se:
- Através da análise descritiva e do diagrama de Pareto, construir o Boxplot determinando se há valores discrepantes.
Passo 1
Nesse problema temos que construir o diagrama de Boxplot da distribuição. Se você não tem muita familiaridade com isso relaxa que eu vou te explicar os pontos principais. Uma figura do tipo Boxplot é assim:
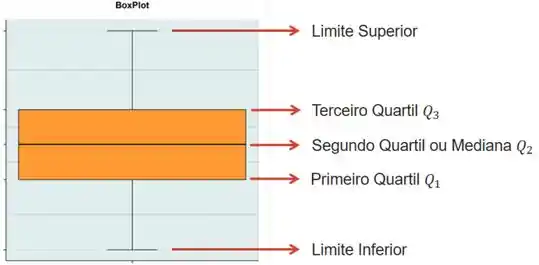
Para fazer diagrama, temos que identificar os quartis e os limites inferior e superior. Nos próximos passos vou detalhar como se faz isso.
Passo 2
Vou dar a ideia básica de como achar os quartis. Para isso, vou dar um exemplo usando uma amostra ordenada:
Essa amostra não tem nada a ver com o problema, estou colocando-a aqui apenas para explicar a ideia. O primeiro quartil é o número que deixa dos dados acima e abaixo. Nesse caso, como temos dados, representa os dois primeiros dados e a fronteira entre esses dados e os demais dados está entre os números e . Vou tomar a média deles como o quartil:
Assim, o primeiro quartil divide a amostra em duas partes: uma com dos valores e a outra com . O segundo quartil é o valor que divide a amostra em duas metades (ele é a famosa mediana). Nesse caso, ele será a média entre e :
Já o terceiro quartil divide a amostra em uma parte com da amostra e outra com , porém diferentemente do primeiro quartil, a amostra com agora representa os maiores valores. Vemos que essa divisão acontece entre o e , de modo que
Espero que esse exemplinho bobo tenha ilustrado para você como a gente pode encontrar os quartis. Agora vamos ao nosso problema!
Passo 3
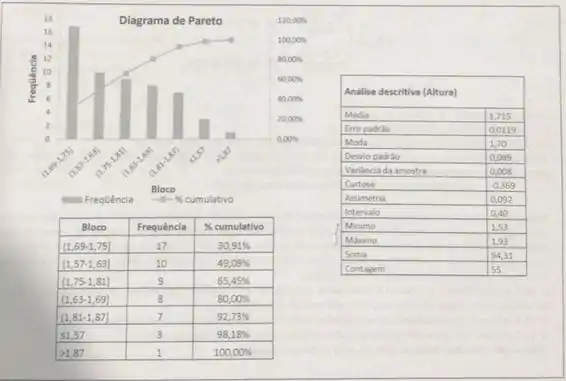
Olhe para a tabela de frequência. Vou dispor os dados em ordem crescente:
Já coloquei também as frequências relativas de cada faixa. Somando as frequências das duas primeiras faixas, achamos
Somando também com a terceira faixa:
Isso significa que o primeiro quartil está nessa faixa. Como não sabemos exatamente o valor de cada altura, temos que dar um jeito de estimar o quartil. Uma forma é simplesmente pegar o ponto médio do intervalo. Vou adotar ela por ser a mais simples:
Seguimos somando a porcentagem de cada faixa:
Como passamos de , isso significa que o segundo quartil (mediana) está nessa faixa:
Continuando, somamos a próxima faixa:
Isso significa que o terceiro quartil está nessa faixa:
Passo 4
Só falta achar os limites inferior e superior, que são definidos por
Desta forma, para obter esses limites temos que calcular primeiro
Olha para a tabela, o mínimo dos dados é um número menor ou igual a . Portanto, o máximo entre esse mínimo e será , de modo que
Já o máximo dos dados é um número maior que , de modo que o mínimo entre esse máximo e é . Portanto,
Com todos esses dados nós já podemos montar o Boxplot:
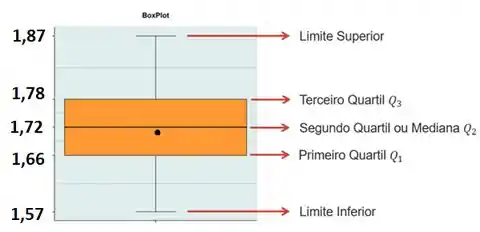
O pontinho preto representa a média (dada na tabela de análise descritiva) que é . Como ela é menor que a mediana, representei ela abaixo. Note também que a distribuição é bem simétrica, já que a distância entre os quartis é simétrica.
Na tabela de análise descritiva também foram fornecidos os valores máximo e mínimos da amostra:
Notar que o máximo é maior que o limite superior e o mínimo é menor que o limite inferior. Esses pontos são valores discrepantes da amostra, pois se encontram fora das barras do Boxplot.
Resposta
Esboço de gráfico.