Construa o Boxplot determinando se valores discrepantes no seguinte conjunto de dados vindo de uma amostra coletada em campo. Plotar todos os valores conforme a aula-1.

Dados:

Organizando nossos dados, ficamos com

Agora vamos definir nossa mediana, e é por ela que sempre iniciamos a contrução de nosso boxplot. Assim tome o valor central de nosso dado. Como temos um número par de dados, vamos pegar o dois centrais e tirar a média.

Felizmente os dois valores centrais são e , assim a média é . Desta forma já iniciamos nosso gráfico definindo nossa mediana em .

Agora vamos calcular e

Tanto quanto representam dos valores mais próximos da Mediana. Entretanto temos que são valores menores que a mediana e são os valores maiores que a mediana.

Assim tome que

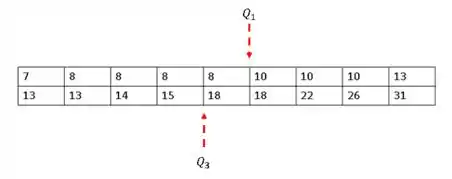
Ou seja e . Assim já podemos desenhar mais esses dois ponto.

O que já nos permite fechar nosso retângulo

“Por fim” vamos definir nossos limites inferiores e superiores.

Devemos desenhar nossas retas pela seguinte regra

Ou seja, suponha que estejamos plotando nosso limite inferior. Então vamos prolongar nossa reta até 1 passo e meio da diferença entre os quartis 1 e 3. Caso o menor valor esteja antes desse 1 passo e meio da diferença, terminamos nosso limite no menor valor, caso não, temos que os ponto que sombram serão considerados discrepantes.

Assim temos que

Ou seja, nosso limite pode chegar até o valor , mas o menor valor é o , assim paramos em mesmo.

E para o limite superior

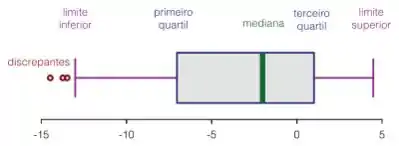
Assim mesmo o ultimo valor sendo nosso limite superior deve parar em . Assim temos apenas como valor discrepante e nosso gráfico boxplot fica

Onde o “asterisco” no final indica que existe um valor discrepante acima de