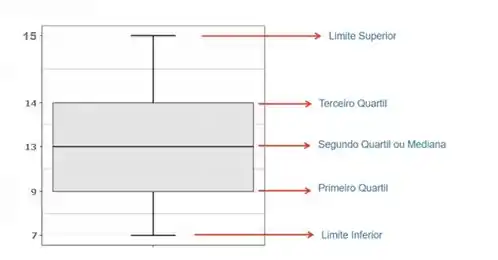
Construa um Boxplot determinando se há valores discrepantes no seguinte conjunto de dados vindo de uma amostra coletada em campo. Plotar todos os valores conforme a aula-1.

Passo 1
Para construir um Boxplot, precisamos dos valores dos 2º, 3º e 4º quartis, e também dos valores das nossas cercas que limitam o gráfico. Vamos calcular essa galera, começando pelos quartis!
A tabela do enunciado já veio bonitinha em ordem crescente, como tem que ser, então já fomos poupados dessa parte!
2º quartil, ou a FAMOSA mediana, é o valor central dos nossos dados. Mas pera, não temos só um valor central nesses dados! Já que temos um número par de valores, vamos ter dois valores centrais!
Como que faz nesse caso mesmo? Nossa mediana vai ser a média aritmética entre os dois valores centrais. Checando na nossa tabela, nossos valores centrais são dois 13, então:
Ok, já temos nossa mediana!
A posição do 1º quartil é dada por:
Onde é nosso número de dados totais, no nosso exemplo temos 18 dados. Então:
Como não existe a “posição 5,25” (posições têm que ser um número inteiro!), vamos ter que fazer uma interpolação entre os valores de posição 5 e posição 6.
Verificando quem são esses valores na tabela... temos a boa notícia de que eles são iguais! Ambos valem 9, e qualquer interpolação entre dois valores iguais é igual a esse mesmo valor!
Então podemos afirmar que:
Poupamos maaais trabalho e continha.
3º e último quartil agora, a posição dele é dada por:
Opa, de novo deu número quebrado. Vendo quem tá na posição 13 e 14 na tabela... Verificamos que são os valores e , então o quartil terá que ser também:
Então nosso 3º quartil vale .
Nosso então é:
Passo 2
Show, agora vamos calcular nossas cercas do Boxplot.
Começando pela cerca inferior:
E agora a superior:
E agora, com as cercas, podemos verificar se temos valores discrepantes, ou seja, valores fora da cerca. E com esses valores podemos descobrir quem vão ser nossos limites superiores e inferiores:
O já é nosso menor valor mesmo, então não temos valores pra fora da cerca inferior.
Opa, não é nosso maior valor, então tem gente pra fora aí! Todos os valores maiores que da tabela de dados são discrepantes: .
Passo 3
Montando o Boxplot:
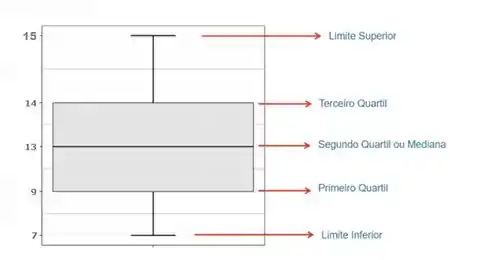
Resposta