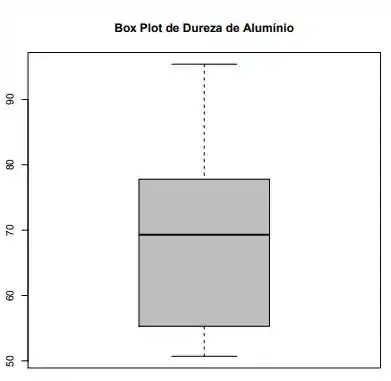
Considere novamente os dados sobre a dureza do alumínio.
Construa o Box-Plot dos dados.
Passo 1
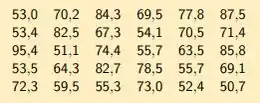
Primeiro colocamos esses dados em ordem:
A mediana é o valor central, como temos dados, a mediana vai ser a média entre a posição e , que é:
O primeiro quartil vai estar na posição:
Fazendo a média ponderada entre os valores de posição e :
Agora o terceiro quartil:
Fazendo a média ponderada entre os valores de posição e 23:
Então o é:
Passo 2
Calculando as cercas:
Olhando nos dados, o menor valor que ainda está dentro da cerca é e não há valores discrepantes para baixo.
O maior valor que ainda está dentro da cerca é e não há valores discrepantes para cima.
Nosso gráfico fica assim então:
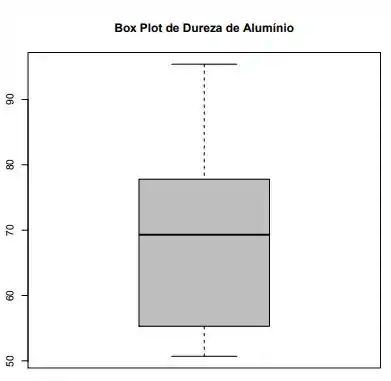
Passo 3
Resposta
Exercícios de Livros Relacionados
Reconsidere os dados de qualidade da agua do exercicio 6.24. Construa um diagrana de caixa dos dados e escreva uma interpretação do grafico. Como o diagrama de caixa se compara, em valor interpretativ
Reconsidere os dados de resistência da solda do Excrcicio 6-23. Construa um diagrama de caixa dos dados e escreva uma interpretação do gráfico. Como o diagrama de caixa se compara, em valor interpreta
Use os dados das alturas dos alunos e das alunas dos Exercícios 6-22 e 6-29 para construir diagramas de caixa comparativos. Escreva uma interpretação da informai-o que você vê nesses diagramas.
O “Tempo de ignição fria” de um motor de carro está sendo investigado por fabricante gasolina. O seguinte tempos (em segundos) foram obtidos emprego de teste: calcule a média, a variância e desvio pad
Um artigo em Nature Genetics(2003,Vol.34(1),pp.85-90)Treatment-specific changes in gene expression discriminate in vivo drug response in human leukemia cells-Mudanças devido a tratamentos específicos