Os dados abaixo correspondem a notas de uma turma de Probest com 30 alunos:
Onde:
(c) Construa um desenho esquemático (boxplot).
Passo 1
Letra c)
Já temos nossos quartis calculados, a única coisa que falta para construirmos o box-plot é calcular nossas cercas inferior e superior. Pra isso, precisamos saber nosso :
Agora partiu calcular as cercas:
E pra finalizar nosso Box-plot, temos que desenhar um retângulo, onde a base desse retângulo coincide com o primeiro quartil, e o topo coincide com o terceiro quartil.
Depois passamos uma paralela ao eixo horizontal na altura da nossa mediana, e duas linhas também paralelas ao eixo horizontal na altura dos últimos valores extremos não discrepantes (últimos valores dentro das cercas). Nesse caso, são os valores e .
Nunca esqueçam que essas retas horizontais exteriores NÃO SÃO AS CERCAS, e sim o maior e o menor valor não discrepante!
Também podemos representar o que é um valor discrepante como um pontinho. No final temos que ter isso aqui:
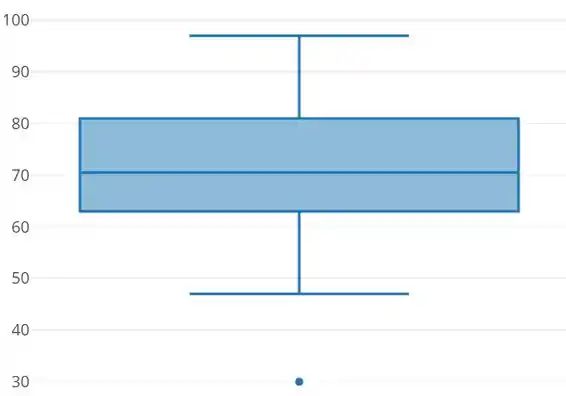
PS: Na hora da prova, não se preocupe em escrever todos os dados da amostra no eixo vertical. Basta escrever o suficiente pra ter ideia de onde estão localizados os quartis e as cercas no gráfico. =)
Resposta
Letra c)