Os dados da tabela abaixo representam o número de acidentes relacionados a uma empresa com dez construções em andamento durante os anos de 2016 e 2017.

(a) Calcule o número médio de acidentes e o desvio padrão do número de acidentes para cada ano.
(b) Calcule os quartis do número de acidentes e construa um box-plot dos dados para cada ano. Os dois box-plots devem aparecer juntos na mesma figura, ou seja, utilize a mesma escala de forma que os gráficos fiquem comparáveis. Existe(m) valor(es) discrepante(s)?
(c) Calcule o coeficiente de correlação.
Passo 1
a)
Vamos começar pelo ano 2016, ou seja, :
Agora 2017, ou :
Passo 2
b)
Primeira coisa é colocar os dados em ordem crescente:
![]()
Agora podemos calcular as posições dos quartis:
O primeiro quartil está estre o 3º e o 4º termo, fazemos uma interpolação:
O segundo quartil está exatamente na posição central entre o 5º e 6º termo, então podemos fazer uma média aritmética simples:
O terceiro quartil está entre o 7º e o 8º termo, fazendo a interpolação:
Então a DIQ vai ser:
Com isso podemos calcular as cercas inferiores e superiores:
Agora temos que olhar se no ano 2016 existe algum valor fora do intervalo . Não tem! Então pra não existe valor discrepante. O maior valor não discrepante é 18 e o menor é o 8.
Olhando agora 2017... existe algum valor fora do intervalo ? Sim! O valor zero. O maior valor não discrepante é o 15 e o menor o 5.
Organizando tudo isso nos gráficos BoxPlot:
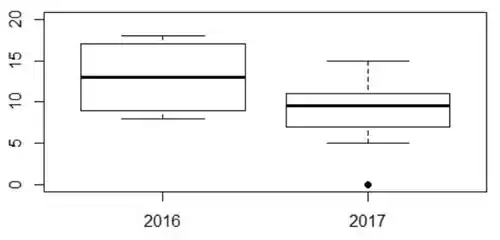
Passo 3
c)
A fórmula do coeficiente de correlação é:
Abrindo isso aí:
Resposta
a)
b)
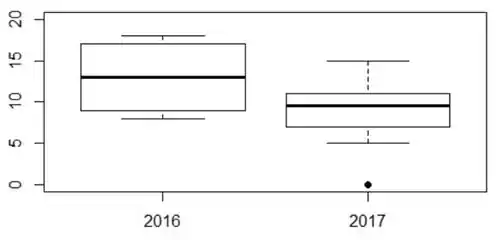
c)