Duas lâmpadas queimadas foram acidentalmente misturadas com seis lâmpadas boas. Se vamos testando as lâmpadas, uma por uma (sem reposição), até encontrar duas defeituosas, qual é a probabilidade de que a segunda defeituosa seja encontrada no quarto teste?
Passo 1
Vamos lá!
Temos um total de 8 lâmpadas: 6 boas (L) e 2 queimadas ()
Essas lâmpadas foram misturadas e devemos testar uma a uma até encontrar as duas defeituosas, ou seja, podemos ter esses casos aqui ô:
1º caso: ou seja, de cara testamos as duas queimadas.
2º caso: testamos a primeira, está queimada, contudo a segundo está boa e a terceira está queimada.
E assim por diante certo?
Maas o enunciado pede a probabilidade de ocorrer um caso em particular, veja só:
Duas lâmpadas queimadas foram acidentalmente misturadas com seis lâmpadas boas. Se vamos testando as lâmpadas, uma por uma, até encontrar duas defeituosas, qual é a probabilidade de que a segunda defeituosa seja encontrada no quarto teste?
Então ele quer o caso em que a segunda defeituosa seja encontrada no QUARTO teste, ou seja, pode ser:
Para resolver esse probleminha vamos usar a permutação com repetição.

Por quê?? Vamos ver agora!!!
Passo 2
Então ele quer o caso em que a segunda defeituosa seja encontrada no QUARTO teste, ou seja, pode ser:
Note que neste caso, os primeiros três testes não estão determinados, contudo o último (o quarto) necessariamente precisa ser uma lâmpada queimada. Podemos dizer então que ela está fixa na quarta posição certo?

Percebemos então que se olharmos apenas para as três primeiras retiradas podemos fazer uma permutação entre essas lâmpadas:
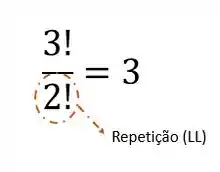
Então sabemos que seja lá qual for a probabilidade, precisaremos multiplicar por três, pois temos três possibilidades desse resultado acontecer.
Passo 3
Agora vamos calcular a probabilidade:
- Probabilidade da primeira lâmpada ser boa:
- Probabilidade da primeira lâmpada ser queimada:
- Probabilidade da segunda lâmpada ser boa, dado que a primeira foi boa:
Probabilidade da segunda lâmpada ser boa, dado que a primeira foi queimada:
Probabilidade da segunda lâmpada ser queimada, dado que a primeira foi boa:
E por ae vai, então percebemos que terá sempre essa cara:
Probabilidade de termos: 2 lâmpadas boas e 2 queimadas:
Probabilidade de na quarta retirada termos a última queimada: