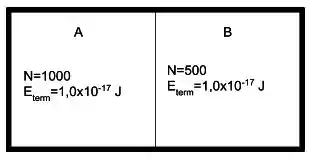
Uma caixa isolada termicamente contém dois compartimentos separados por uma membrana fina. Os dois compartimentos contêm o mesmo gás monoatômico, porém nas condições indicadas na figura ao lado. Sendo a velocidade quadrática média e a energia térmica total, podemos afirmar:
- ,
- ,
- ,
- ,
- ,
Passo 1
Vamos lá! Essa questão é puramente teórica e aborda conceitos de Cinética dos Gases. Então para resolve-la, que tal lembrarmos do conceito do Teorema da equipartição de energia? Esse teorema nos diz que para uma molécula monoatômica a energia total de cada molécula vale:
Onde a energia cinética média é:
Note que é proporcional a que é energia cinética média de uma molécula e não a energia cinética média total.
O enunciado nos diz que os dois gases têm a mesma total. Porém, o gás contém mais moléculas do que o gás , então a Energia cinética por molécula no gás é menor do que a Energia cinética por molécula no gás .
Assim, analisando as equações descritas anteriormente, podemos ver que o gás ao possuir menor implica que sua e sua é menor que no gás .
Resposta
Letra B.