Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cinética dos Gases

Ver Teoria
Exercício 301234567891011121314151617181920212223242526272829313233343536373839404142434445464748

Enunciado

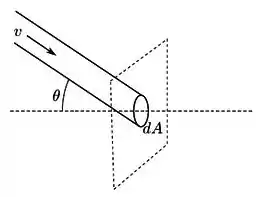
Um feixe de moléculas idênticas de massa m e velocidade v → está direcionado para uma parede, em um ângulo θ com a normal à parede. O feixe possui n moléculas por unidade de volume e atinge a parede sobre uma área dA, como mostrado na figura. Qual é a pressão que o feixe exerce sobre a parede?

(a) 2 m n ( v   c o s   θ ) 2 .

(b)   m n ( v   c o s   θ ) 2 .

(c) 2 m n ( v   c o s   θ ) 2 dA.

(d) 2 m n v   c o s   θ .

(e)   m n v   c o s   θ .

Passo 1

A força é a variação do momento linear sobre o tempo. Podemos escrever:

F → = ∆ Q ∆ t

Beleza! Vamos pensar na variação do momento linear então. Inicialmente as moléculas tem uma velocidade v x → =   v → cos ⁡ θ . Elas colidem com a parede, e voltam com uma velocidade - v x → = -   v → cos ⁡ θ . Então:

F → = ∆ Q ∆ t = v x → M - - v x → M ∆ t

F → = 2 v x → M ∆ t

F → = 2 v → cos ⁡ θ M ∆ t

Show! E nós podemos escrever:

M V = m n

Ou seja: a massa total de moléculas sobre o volume é igual à massa de uma molécula vezes o número de moléculas por unidade de volume.

E o volume podemos escrever:

V = l d A

Sendo l o comprimento do feixe na direção x. Então:

M = m n l d A

Então:

F → = 2 v → cos ⁡ θ m n l d A ∆ t

Passo 2

Como:

v x → = l / ∆ t

Podemos trocar:

F → = 2 v → cos ⁡ θ v → cos ⁡ θ m n d A

F = 2 v cos ⁡ θ 2 m n d A

E como:

P = F / A

P = 2 v cos ⁡ θ 2 m n d A d A

P = 2 m n v cos ⁡ θ 2

Resposta

Letra A.

Exercícios de Livros Relacionados

A água a céu aberto a 32° C evapora por causa do escape de algumas moléculas da superfície. O calor de vaporização ( 539c a l / g ) é aproximadamente igual a ε n , onde ε é a energia média das molécul
Com que frequência as moléculas de oxigênio ( O 2 ) colidem à temperatura de 400K e a uma pressão de 2,00a t m ? Suponha que as moléculas têm 290p m de diâmetro e que o oxigênio se comporta como um gá
Calcule a integral da Equação (18.30), ∫ 0 x v f vd v e compare o resultado com v 2 m é d é como dada pela Equação (18.35). (Sugestão: faça a mudança de variável v 2 = x e use a integral tabelada ∫ 0
O oxigênio ( O 2 ) é confinado a um recipiente em forma de cubo de 15c m em uma borda a uma temperatura de 300K .
O oxigênio tem uma massa molar de 32 g/mol e o nitrogênio tem uma massa molar de 28 g/mol. As moléculas de oxigênio e nitrogênio em uma sala têm(a) energias cinéticas translacionais médias iguais, mas