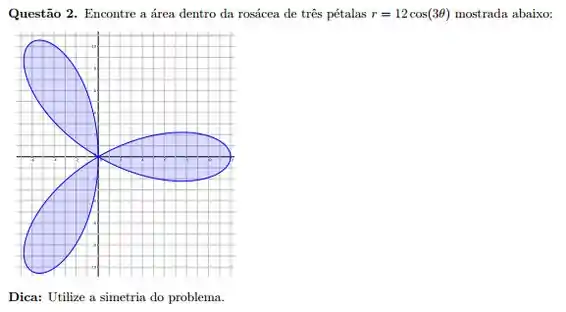
Passo 1
Essa questão aqui é clássica de curvas polares. Ou seja, o enunciado vai te dar uma curva já escrita em curvas polares e te pedir alguma integral.
O difícil aqui é pegar esse informação e transformar em
Pra isso a gente tem que lembrar da mudança original para coordenadas polares:
Onde é a distância de algum ponto até a origem e o ângulo é aquele da trigonometria mesmo, que começa no eixo e roda de até , assim:
Sabendo isso, como queremos a região interior a , os limites de são
Ué, mas por que começa em ?
Dá pra identificar isso procurando se a curva passa na origem. Como no nosso esboço do enunciado ela passa e queremos todo o interior da curva, podemos dizer que o raio começa em zero.
Passo 2
Mas então e os limites de , como a gente faz? Como usamos a tal simetria que o enunciado deu de dica?
A simetria que ele fala é a seguinte:
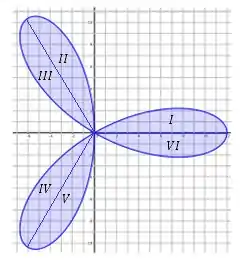
Temos seis regiões com a mesma área! Então só precisamos analisar uma delas e multiplicar por !
Vou dar um zoom aqui na região então
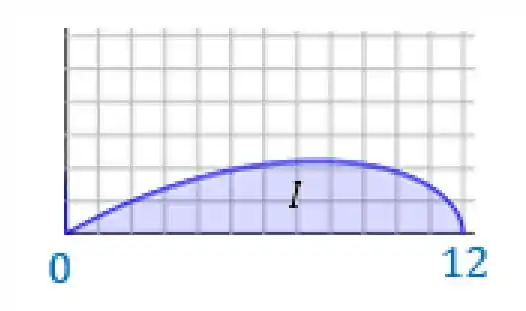
Percebe que a curva vai de até . Não só isso, analisando melhor o , que é a distância até a origem, temos que
É muito importante lembrar que esse zoom que dei foi no primeiro quadrante! Então só estamos pensando em
Logo
Passo 3
Juntando tudo que temos na integral de área dos seis pedaços simétricos, ficamos com
Não se esqueça do jacobiano de coordenada polar que vale , temos:
Passo 4
Integrando em
Para integrar em , precisamos lembrar da relação trigonométrica que diz
Voltando pra integral
Agora sim podemos integrar em
Como , temos que