Utilizando integral dupla em sistemas de coordenadas polares, determinar a área da região delimitada pela curva com equação:
Dica:
Passo 1
Na hora da prova é bem difícil ter tempo de esboçar essa superfície bizarra aí né? Vamos tentar entender como fazer isso sem esboço, beleza?
O enunciado fala pra gente usar coordenadas polares, vamos jogar isso ali e ver o que sai! As coordenadas são essas aqui
Dividindo por nos dois lados
Usando a substituição do enunciado:
Logo, sabemos que
Passo 2
Como nossa região não tem nenhuma restrição de ou positivos, temos que percorrer de algum intervalo de para pegar o todo.
Do limite de , temos que:
Sabendo disso, temos que
Então o gráfico disso vai ser igual ao do cosseno, só que com período . Assim:
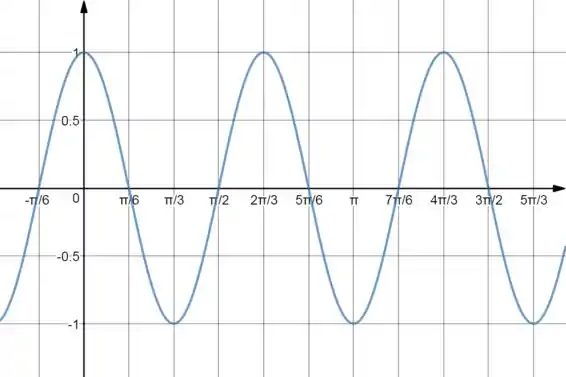
Então, dentro de um intervalo de , temos que vai ser maior que para os seguintes intervalos:
Viu! Conseguimos todos os limites sem o esboço dessa região maluca. Se você realmente ficou curioso, o esboço feito no computador é esse aqui
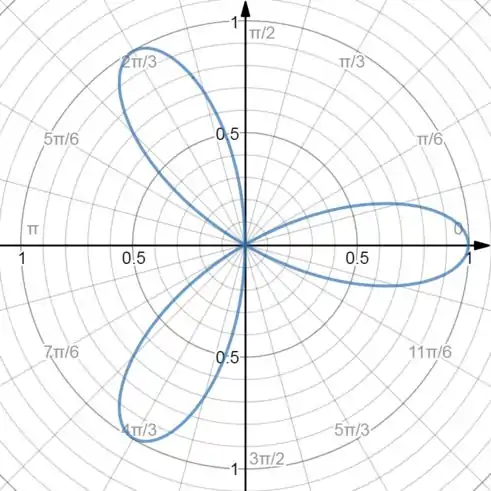
Mas realmente não precisamos perder muito tempo nisso na hora da prova, às vezes nem precisamos do esboço =D
Passo 3
Bom, agora que definimos a região em coordenadas polares, calcular a área é calcular a integral dupla, certo?
Não se esqueça do jacobiano, beleza?
Passo 4
As três integrais em são idênticas, logo
Pra integrar isso aí em relação a , vamos lembrar da relação que diz
Logo
Vamos fazer as três separadamente
A segunda integral fica
A terceira e última fica
Somando tudo