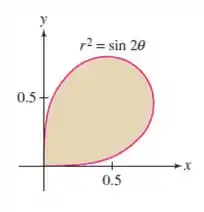
Calcule a área da região delimitada pela lemniscata mostrada na figura abaixo.
Passo 1
Para encontrar a área dessa região faremos:
Onde é justament a região descrita no enunciado. Olhando a imagem conseguimos notar que a região esta apena no primeiro quadrante, então temos a variação de . Já para análise da variação do r, simplesmente isolamos ele na função.
Passo 2
Montando então a integral ficamos com:
Resposta
Exercícios de Livros Relacionados
Cardioide no primeiro quadrante: Encontre a área da região cortada do primeiro quadrante pela cardioide r=1+s e n ( θ ) .
Encontre a área da região cortada do primeiro quadrante pela curva r = 2 2 - s e n 2 θ 1 2 .
Uma pétala de rosa: Encontre a área delimitada por uma pétala da rosa r=12c o s( 3 θ ) .
Concha de caracol: Encontre a área da região delimitada pelo eixo x positivo e a espiral r= 4 θ 3 ,0≤ θ≤2 π . A região se assemelha a uma concha de caracol.
Encontre a área da região comum aos interiores das cardioides r=1+c o s ( θ ) er=1–c o s ( θ ) .