A Lemniscata de Bernoulli é a curva algébrica do quarto grau de equação cartesiana:
A Lemniscata é a figura geométrica com a forma de uma hélice, similar ao numeral e ao símbolo de infinito . Pode ser descrita por coordenadas polares:
Calcular a área dentro da Lemniscata:
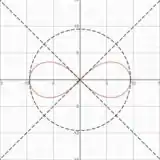
Sabendo que no primeiro quadrante deve-se considerar e .
Passo 1
Essa seria uma questão bastante complicada, mas por sorte o enunciado já deu os limites de integração.
Como os dois “lados” da figura são iguais, é suficiente calcular a área de um deles, para então multiplicá-la por dois.
Como queremos calcular uma área, nosso objetivo é montar uma integral como essa:
Ou seja, precisamos achar e .
Passo 2
A região fica definida pelos limites de integração, mas como dissemos antes, eles já foram dados pela questão:
E o depende do sistema de coordenadas que estamos usando! No caso de coordenadas cartesianas, seria:
Mas nas coordenadas polares, precisamos considerar o jacobiano, que no caso das coordenas polares dá:
Agora já podemos substituir isso tudo na integral:
E se resolvermos essa integral, teremos a área de um dos lados daquela figura.
Passo 3
Começamos integrando o :
Agora vamos arrumar essa integral antes de resolvê-la:
Passo 4
Calcular a integral do exige uma identidade trigonométrica muito importante:
Vamos ver como fica a integral (indefinida) de disso:
E essas duas integrais são bem mais fáceis!
Então:
Substituindo os limites de integração:
Agora vamos arrumar um pouco essa equação:
Ou seja:
Passo 5
Agora só precisamos lembrar do que falamos antes: essa área que foi calculada é só de uma metade de figura. A área que a questão pediu é, na verdade, o dobro dessa:
Pronto!
Resposta
A área dentro da Lemniscata é .