Calcule a área de um laço da rosácea cuja equação em coordenadas polares é .
Passo 1
Bom, para você ter uma ideia, essa rosácea é assim:
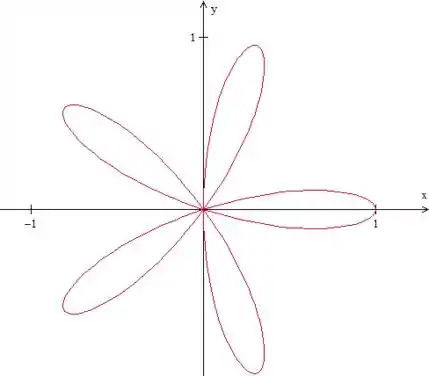
Passo 2
Mas a questão pede a área de apenas um laço. Bom, tá na cara que é para usarmos coordenadas polares, né? O problema já deu a curva na forma polar.
Então vamos pensar nos intervalos. O de é fácil, o raio varia desde a origem até a curva , logo, .
O de temos que pensar um poquinho. O que “define” uma pétala não é a curva passar pela origem. Digo, toda vez que ela vai e volta para a origem temos uma nova pétala. E a curva passa pela origem cada vez que o raio se anula, não é?
Então o intervalo de que marca uma pétala é aquele que faz duas vezes.
Os dois primeiros valores de que fazem são, portanto:
Logo, .
Passo 3
Agora vamos montar ai integral com o que encontramos:
Não se esqueça desse do Jacobiano!
Passo 4
Agora vamos integrar isso ái
Agora precisamos usar essa identidade
Aplicando ao nosso problema, temos: