Ache a massa da lâmina na forma da região exterior à limaçon e interior à circunferência , se a densidade de massa por unidade de àrea em qualquer ponto for .
Passo 1
Vamos começar fazendo um desenho dessa região para entender melhor o que está acontecendo.
O esboço das regiões é esse aqui em baixo: Mas na prática você não precisa saber desenhar isso (ninguém sabe desenhar uma limaçon haha)
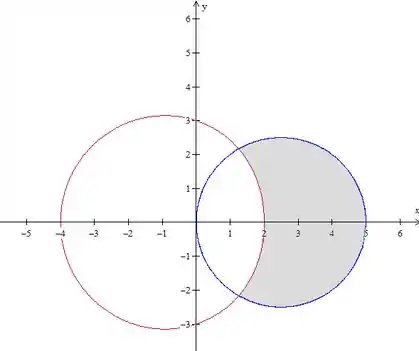
O que o problema pede é então o seguinte:
Onde é a região em cinza que vimos na figura.
Passo 2
Agora precisamos descrever a região. E como o problema já nos dá as equações em coordenadas polares, vamos usar coordenadas polares né.
Já temos a função densidade de área em coordenadas polares também, então a integral fica o seguinte:
Pela figura, vemos que varia desde a equação da circunferência vermelha até a da azul . Agora falta descobrir o intervalo de , para isso, vamos fazer a interseção entre as duas curvas:
Assim, sabemos que e a integral fica:
Ou podemos escrever:
Por causa da simetria da figura.
Passo 3
Agora vamos resolver essa integral ai, começando integrando em relação a :
Como o seno é positivo para os valores de da integral, podemos retirar esse módulo sem problemas:
Passo 4
Agora vamos integrar em relação a .