Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Curvas Polares

Ver Teoria
Exercício 61234578910111213141516

Enunciado

Calcule a área da região do plano x y interior à curva r = 2 1 - cos ⁡ θ e exterior à curva r = 3 , onde as mesmas estão descritas em coordenadas polares.

Passo 1

O segredo aqui é montar uma integral dupla em coordenadas polares para calcular essa área. E como a gente faz isso? Bora ver!

Para fazer essa integral a gente precisa limitar r e θ para essa região.

O enunciado diz que nosso região está dentro da curva

r = 2 1 - cos ⁡ θ

Aí a gente escreve essa região assim:

r ≤ 2 1 - cos ⁡ θ

Isso que dizer que nosso valor de r deve ser menor ou igual ao valor de r dessa curva. Ou seja, deve estar dentro dela.

E ele diz que estamos fora de r = 3 . Isso é um circulo de raio 3 . Para estarmos fora desse circulo, nosso raio r precisa ser maior que 3 , certo? Então para representar isso, a gente escreve

r ≥ 3

Com isso a gente limita o r :

3 ≤ r ≤ 2 1 - cos ⁡ θ

Passo 2

Para limitar θ , precisamos fazer a interseção entre essas duas curvas. Aí a gente tem:

r = 2 1 - cos ⁡ θ ,     r = 3

2 1 - cos ⁡ θ = 3

1 - cos ⁡ θ = 3 2 ∴ 1 - 3 2 = cos ⁡ θ ∴ cos ⁡ θ = - 1 2

θ = a r c c o s   - 1 2

A gente sabe que um ângulo cujo o cosseno é 1 / 2   é π / 3 . Então para achar os ângulos que tem - 1 / 2 , vamos espelhar esse π / 3 em relação a y e x . Assim:

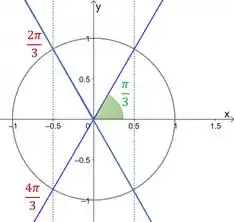
Já que o cosseno é negativo na parte esquerda do gráfico. Os ângulos que a gente quer são esses

θ 1 = 2 π 3 , θ 2 = 4 π 3

Aí podemos escrever:

2 π 3 ≤ θ ≤ 4 π 3

Passo 3

Aí para calcular área a gente sabe que tem que calcular a integral dupla:

A = ∫ ∫ D 1 d x d y

Mas aí aplicando a mudança de coordenadas polar, a gente pôe nossas variáveis r e θ , seus extremos de integração e multiplica o integrando por j a c = r :

A = ∫ 2 π 3 4 π 3 ∫ 3 2 1 - cos ⁡ θ r d r d θ

Repara que a gente integra em relação a r primeiro porque essa variável está entre funções.

Passo 4

Agora é calcular essa belezura:

A = ∫ 2 π 3 4 π 3 ∫ 3 2 1 - cos ⁡ θ r d r d θ

A = ∫ 2 π 3 4 π 3 r 2 2 3 2 1 - cos ⁡ θ d θ = 1 2 ∫ 2 π 3 4 π 3 2 1 - cos ⁡ θ 2 - 9 d θ

A = 1 2 ∫ 2 π 3 4 π 3 2 - 2 cos ⁡ θ 2 - 9 d θ = 1 2 ∫ 2 π 3 4 π 3 4 - 8 cos ⁡ θ + 4 cos 2 ⁡ θ - 9 d θ

A = 1 2 ∫ 2 π 3 4 π 3 - 8 cos ⁡ θ + 4 cos 2 ⁡ θ - 5 d θ = 1 2 -   8   s e n   θ 2 π 3 4 π 3 + 4 ∫ 2 π 3 4 π 3 cos 2 ⁡ θ d θ - 5 4 π 3 - 2 π 3

A = 1 2 8 3 + 4 ∫ 2 π 3 4 π 3 cos 2 ⁡ θ d θ - 10 π 3 =

Passo 5

Falta só aquela integral do meio. Aqui a gente usa a identidade:

cos 2 ⁡ θ = 1 + cos ⁡ 2 θ 2

∫ 2 π 3 4 π 3 cos 2 ⁡ θ d θ = ∫ 2 π 3 4 π 3 1 + cos ⁡ 2 θ 2 d θ = 1 2 ∫ 2 π 3 4 π 3 1 d θ + 1 2 ∫ 2 π 3 4 π 3 cos ⁡ 2 θ d θ = π 3 + 1 2 ∫ 2 π 3 4 π 3 cos ⁡ 2 θ d θ

E fazendo a substituição simples u = 2 θ , achamos

∫ 2 π 3 4 π 3 cos ⁡ 2 θ d θ = s e n   2 θ 2 2 π 3 4 π 3 = s e n 8 π 3 2 - s e n 4 π 3 2 = 3 2

∴

∫ 2 π 3 4 π 3 cos 2 ⁡ θ d θ = π 3 + 1 2 3 2 = π 3 + 3 4

Voltando para a nossa área:

A = 1 2 8 3 + 4 π 3 + 3 4 - 10 π 3 = 1 2 8 3 + 4 π 3 + 3 - 10 π 3

A = 1 2 9 3 - 6 π 3 = 1 2 9 3 - 2 π

Resposta

A = 1 2 9 3 - 2 π

Exercícios de Livros Relacionados

Cardioide no primeiro quadrante: Encontre a área da região cortada do primeiro quadrante pela cardioide r=1+s e n ( θ ) .
Encontre a área da região cortada do primeiro quadrante pela curva r = 2 2 - s e n 2 θ 1 2 .
Uma pétala de rosa: Encontre a área delimitada por uma pétala da rosa r=12c o s( 3 θ ) .
Concha de caracol: Encontre a área da região delimitada pelo eixo x positivo e a espiral r= 4 θ 3 ,0≤ θ≤2 π . A região se assemelha a uma concha de caracol.
Encontre a área da região comum aos interiores das cardioides r=1+c o s ⁡ ( θ ) er=1–c o s ⁡ ( θ ) .