Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Curvas Polares

Ver Teoria
Exercício 51234678910111213141516

Enunciado

  1. Exprima (sem calcular)

∫ 0 π 4 ∫ sec ⁡ θ 2 cos ⁡ θ r 2 1 + r sin ⁡ θ   d r d θ

como integral iterada em coordenadas retangulares, nas duas possíveis ordens de integração.

Passo 1

Bem! Tenho que e falar para não se assustar com exercícios de retorno às integrais retangulares como esse, pois basicamente ele vai seguir a mesma linha de resolução, ou seja, teremos que desenhar a região em primeiríssimo lugar!

Todavia, como ele está em coordenadas polares, devemos relembra-las para prosseguir, ok?

x = r cos ⁡ θ

y = r sin ⁡ θ

Uma equação que nos ajuda muito é a equação da circunferência...

x 2 + y 2 = r 2

E, claro, o Jacobiano:

J = r

Passo 2

Pois bem, pra desenhar a região vamos como sempre devemos fazer, obter as informações da integral onde concluímos que, como d r vem primeiro, r varia no intervalo mais interno da integral dupla

sec ⁡ θ ≤ r ≤ 2 cos ⁡ θ

enquanto θ ...

0 ≤ θ ≤ π 4

Com essas informações, obtemos 4 equações fundamentais para a resolução do problema

r = sec ⁡ θ

r = 2 cos ⁡ θ

θ = 0

θ = π 4

O que vamos fazer agora vai ser basicamente trabalhar com essas quatro equações para chegar a equações que conhecemos e sabemos desenhar (no caso, em termos de x e y ). Bora?

Passo 3

Vamos trabalhar com a primeira equação

r = sec ⁡ θ

Cara! Como queremos chegar a equações envolvendo x e y , o que vamos fazer basicamente será substituir as polares aí. Veja só:

Em r = sec ⁡ θ , podemos falar que

r = sec ⁡ θ = 1 cos ⁡ θ

Passando esse cosseno pro outro lado...

r ∙ cos ⁡ θ = 1

RARA! Quem é r cos ⁡ θ ? Exato! x ! Logo...

x = 1

Já temos a nossa primeira equação que conhecemos, ou seja, essa reta paralela a y aqui ohhh:

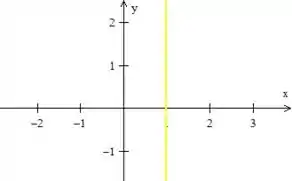
Passo 4

Vamos agora trabalhar com a segunda equação

r = 2 cos ⁡ θ

Poxa! Tem um cosseno ali no segundo membro, além disso, sabemos das coordenadas polares que

r cos ⁡ θ = x           ⇒ P o r t a n t o   i s o l a n d o o   c o s s e n o …             cos ⁡ θ = x r

substituindo então...

r = 2 cos ⁡ θ         →             r = 2 x r         →

r 2 = 2 x

Epa!!! r 2 = x 2 + y 2 …

x 2 + y 2 = 2 x

Só que espera um minuto! Essa equação que chegamos aí tá com cara de circunferência, não está? Vamos trabalhar mais um pouco...

x 2 - 2 x + y 2 = 0                     ⇒ C o m p l e t a n d o   q u a d r a d o   e m   x                     x 2 - 2 x + 1 + y 2 - 1 = 0

ATENÇÃO 1: Esses três termos em negrito vira um quadrado perfeito x - 1 2 . Por isso o truque de adicionar 1 e tirar 1 , pegou?

x - 1 2 + y 2 - 1 = 0     →

x - 1 2 + y 2 = 1

Nossa! Estamos de fato trabalhando com uma circunferência de raio 1 , porém deslocada de uma unidade a direita em x !

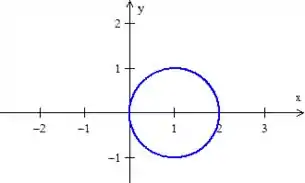
ATENÇÃO 2: Esse truque que utilizamos é muuuuuuito utilizado e os professores adoram essa circunferência, por isso é bom ter esse truque no sangue, ta ok? :)

Passo 5

Concluímos as equações de r , mas falta-nos trabalhar com as equações de θ :

θ = 0

θ = π 4

E cara, aqui dá pra você obter as retas bonitinhas substituindo como fizemos, mas também dá pra você fazer beeeeem mais rápido apenas lembrando quem é esse ângulo aí!

Ora! Esse ângulo é esse aqui, ohh:

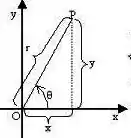
Logo θ = 0 representa o próprio eixo x (onde y = 0 ) e θ = π 4 = 45 ° é uma reta que tá na metade do primeiro quadrante aí, ou seja: y = x . Sacou?

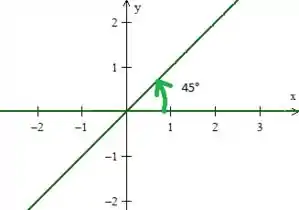
Como quando x = 1 , y = 1 , o ângulo θ “varre” exatamente esse um quarto da esfera hachurado!

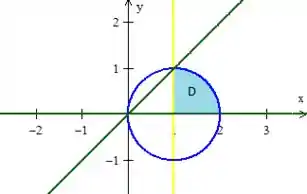
Que no caso, é região !

Passo 6

Região encontrada, basta descrevê-la usando os dois Tipos! Vamos começar aqui com o Tipo 1 :

x deve variar em um intervalo numérico bem definido, no caso...

1 ≤ x ≤ 2

Enquanto que y deve variar da base até esse pedacinho positivo da circunferência

0 ≤ y ≤ C i r c u n f e r ê c i a   a z u l

Como a “circunferência azul” tem equação x - 1 2 + y 2 = 1 , isolando o y ...

y 2 = 1 - x - 1 2     →           y = ± 1 - x - 1 2

Como só queremos o pedaço de cima...

0 ≤ y ≤ 1 - x - 1 2

Passo 7

Como o problema quer a integral escrita das duas formas temos que descrevê-la também como do t i p o   2 :

Aqui o y varia em um intervalo numérico bem definido:

0 ≤ y ≤ 1

enquanto que x ...

R e t a ≤ x ≤ C i r c u n f e r ê n c i a   a z u l

1 ≤ x ≤ C i r c u n f e r ê n c i a   a z u l

A circunferência tem equação x - 1 2 + y 2 = 1 . Isolando agora o x

x - 1 2 = 1 - y 2             →             x - 1 = ± 1 - y 2

x = 1 ± 1 - y 2

Queremos também a parte de lá, logo a positiva...

1 ≤ x ≤ 1 + 1 - y 2

Passo 8

Uma outra coisa muuuuuito importante aqui é transformar também a função que estamos trabalhando em coordenadas polares

r 2 1 + r sin ⁡ θ

para coordenadas cartesianas.

O único cuidado que se deve tomar aqui é que um daqueles r lá em cima é do J a c o b i a n o   ( J = r ) ...

r 2 1 + r sin ⁡ θ = r 1 + r sin ⁡ θ ∙ J

Separado esse Jacobiano, e não se esqueça dele, pode-se substituir naturalmente usando a informação do P a s s o   1

r 1 + r sin ⁡ θ = x 2 + y 2 1 + y

Passo 9

Finalmente com o T i p o   1 do passo 6 ...

1 ≤ x ≤ 2

0 ≤ y ≤ 1 - x - 1 2

Montamos a primeira integral

∫ 0 π 4 ∫ sec ⁡ θ 2 cos ⁡ θ r 2 1 + r sin ⁡ θ   d r d θ = ∫ 1 2 ∫ 0 1 - x - 1 2 x 2 + y 2 1 + y d y d x

Com o T i p o   2 do passo 7 ...

0 ≤ y ≤ 1

1 ≤ x ≤ 1 + 1 - y 2

Montamos a segunda...

∫ 0 π 4 ∫ sec ⁡ θ 2 cos ⁡ θ r 2 1 + r sin ⁡ θ   d r d θ = ∫ 0 1 ∫ 1 1 + 1 - y 2 x 2 + y 2 1 + y d x d y

Resposta

1 - ∫ 1 2 ∫ 0 1 - x - 1 2 x 2 + y 2 1 + y d y d x

2 - ∫ 0 1 ∫ 1 1 + 1 - y 2 x 2 + y 2 1 + y d x d y

Exercícios de Livros Relacionados

Cardioide no primeiro quadrante: Encontre a área da região cortada do primeiro quadrante pela cardioide r=1+s e n ( θ ) .
Encontre a área da região cortada do primeiro quadrante pela curva r = 2 2 - s e n 2 θ 1 2 .
Uma pétala de rosa: Encontre a área delimitada por uma pétala da rosa r=12c o s( 3 θ ) .
Concha de caracol: Encontre a área da região delimitada pelo eixo x positivo e a espiral r= 4 θ 3 ,0≤ θ≤2 π . A região se assemelha a uma concha de caracol.
Encontre a área da região comum aos interiores das cardioides r=1+c o s ⁡ ( θ ) er=1–c o s ⁡ ( θ ) .