Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Densidade

Ver Teoria
Exercício 6123457891011121314151617

Enunciado

Uma esfera oca de 100 cm de diâmetro externo e 40 cm de diâmetro interno possui massa igual a 200 g.

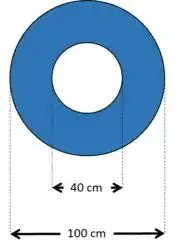
Calcule:

  1. Sua densidade, em k g / m 3 ;
  2. Sua massa específica, também em k g / m 3 .

Passo 1

Aqui você precisa lembrar que para a densidade ( d ) nós usamos o volume total, já para a massa específica ( ρ ), nós excluímos o volume oco!

d = m V t o t a l

ρ = m V t o t a l - V o c o

Passo 2

  1. Densidade

    2. O volume de uma esfera é

    V e s f e r a = 4 3 π r 3

    Como o diâmetro externo é 100 cm, então

    r = 50   c m = 0,5   m

    Jogando na densidade

    d = m 4 3 π r 3

    d = 0,2 4 3 π   0,5 3

    d = 0,38   k g / m 3

    Passo 3

  2. Massa específica

Agora temos que lembrar de excluir o volume oco, que também é uma esfera, só que de diâmetro 40 cm (raio 20 cm).

ρ = m 4 3 π r e x t e r n o 3 - r i n t e r n o 3

ρ = 0,2 4 3 π ( 0,5 3 - 0,2 3 )

ρ = 0,41   k g / m 3

Resposta

  1. d = 0.38   k g / m 3
  2. ρ = 0,41   k g / m 3

Exercícios de Livros Relacionados

Dois corpos esféricos diferem em tamanho e massa. O corpo A tem uma massa que é oito vezes a massa do corpo B. O raio do corpo A é o dobro do raio do corpo B. Como suas massas específicas se comparam?
Determine a massa de uma esfera maciça de chumbo com um raio de 2,00 cm.
Considere uma sala medindo 4,0mx5,0mx4,0m . Sob condições atmosféricas normais, na superfície da Terra, qual é a massa do ar dentro da sala?
Dois corpos diferem em massa específica e em massa. O corpo A tem uma massa que é oito vezes a massa do corpo B. A massa específica do corpo A é quatro vezes a massa específica do corpo B. Como os vol
05. Duas esferas uniformes, uma de chumbo e outra de alumínio, possuem a mesma massa. Qual é a razão entre o raio da esfera de alumínio e o raio da esfera de chumbo?