UFRJ – Física 1 – P1 – 2022.2 – Questão 6.
6) Arquimedes.
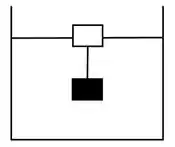
Dois cilindros maciços de volumes idênticos são presos um ao outro por um fio e imersos num recipiente com água, como na figura. O fio que os une é inextensível e tem massa desprezível. Um dos cilindros tem densidade , o outro tem densidade e a densidade da água é de tal forma que . Suponha e fixos; qual a máxima densidade para impedir que too o conjunto que se precipite e vá ao fundo do recipiente? Expresse seu resultado em termos de e .
a.
b.
c.
d.
e.
Passo 1
Fala aí, galerinha! Tudo belezinha com vocês?
Bom, essa questão deu pra gente dois cilindros que estão em equilíbrio dentro de um fluido. E pediu o valor máximo de para que o sistema continue equilibrado.
Para casos como esses sempre devemos fazer o diagrama do corpo livre para cada um dos corpos e analisar direitinho as força que estão envolvidas em todo o processo.
Então, vem comigo que faremos isso juntos.
Passo 2
Para o primeiro corpo, temos:
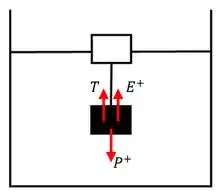
Como o sistema está em equilíbrio, podemos dizer que:
Isolando a tração temos:
E para o outro cilindro, teremos:
E poderemos escrever:
E isolando a tração nessa equação também, ficamos com:
Igualando as duas equações de tração, ficaremos com:
Maravilha, agora vamos analisar o que está acontecendo aqui
Passo 3
Quando o cilindro está na iminência de afundar, todo o seu volume estará submerso no líquido, de modo que poderemos calcular o Empuxo usando a relação:
Da mesma maneira pra o outro cilindro, teremos:
E o peso pode ser expresso por:
E
Substituindo tudo que encontramos, ficaremos com:
Assim
Assim:
E prontinho, encontramos nossa resposta.
Resposta
Resposta:
c.