Considere o octaedro regular (isto é, cujas faces são triângulos equiláteros) de vértices , conforme a figura
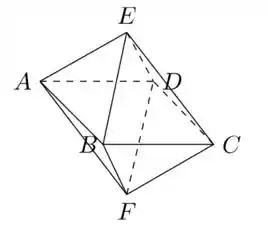
Sabendo que e que a segunda coordenada de é positiva, se é o plano que contém os pontos e é o ponto de mais próximo de , então é igual a
a) 6
b) 2
c) 5
d) 4
e) 3
Passo 1
Fala turma, belezinha?? Vamos lá entender esse exercício
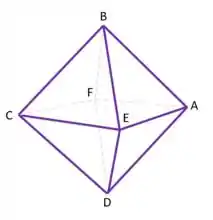
Pra começar, ele dá um octaedro que vou mostrar de forma mais visual aqui pra vocês:
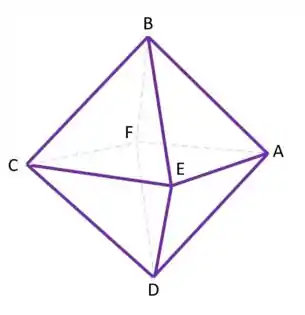
Esse octaedro é regular e cada letra representa um vértice dele. E aí sabemos as coordenadas de alguns pontos:
Além disso, tem um plano que contém os pontos e . Ou seja, ele contém o triângulo equilátero . Nesse plano , temos o ponto , que é o ponto mais próximo do ponto .
E aí o que queremos encontrar são as coordenadas , do ponto , para aí calcularmos

Tem duas chaves que precisamos para resolver esse exercício:
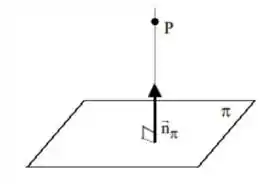
- A menor distância entre um ponto e um plano é a distância ortogonal ao plano. Ou seja, a distância que está na direção do vetor normal. Assim olha:
- Além disso, como é um octaedro regular, precisamos lembrar que , , beleza?
Show!! Dito isso, o passo a passo para resolvermos esse problema é:
- Encontrar a equação do plano (com isso, saberemos o seu vetor normal )
- Encontrar as coordenadas do ponto (lembrando que a segunda coordenada dele é positiva)
- O ponto vai ser a intersecção do plano com a reta que passa pelo ponto e tem vetor diretor
Passo 2
Vamos começar com as informações mais básicas que temos:
Com isso, podemos encontrar os vetores:
Agora dá uma olhada na figura do octaedro:
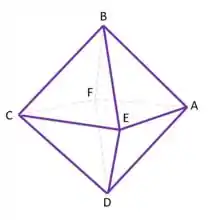
Concorda que é paralelo a ? E também possuem o mesmo tamanho! Afinal, o octaedro é regular, simétricozinho
Show! Então podemos falar que o vetor que vai de até é o mesmo vetor que vai de até :
Portanto
Uhuuu, então já temos as coordenadas do ponto também!!
Passo 3
Para encontrarmos a equação do plano , já temos um vetor diretor: o vetor . Também sabemos que o plano passa pelos pontos e . Masss isso ainda não é suficiente para encontrarmos a equação. Precisamos das coordenadas do ponto também!
Vamos chamar
Como o octaedro é regular, todas as arestas têm que ter o mesmo tamanho, certo? Por exemplo, pegando o tamanho do vetor :
Então necessariamente TODAS as arestas devem medir
Vamos pegar 3 arestas que passem pelo ponto :
Sabemos que o tamanho de todas essas arestas deve ser . Então, podemos montar o sistema:
Elevando os dois lados ao quadrado:
Legal, vamos guardar esse sistema pra usar daqui a pouco.
Também sabemos que as arestas e são perpendiculares. Então o produto escalar entre elas vale :
Logo, temos que
Passo 4
Legal, estamos querendo encontrar as coordenadas de para chegarmos na equação do plano
Sabemos que
E que
Substituindo isso na segunda equação do sistema:
Ebaaa, já temos a primeira coordenada!!
Substituindo nas outras equações:
Subtraindo as duas equações:
Então:
Opa, então o ponto pode ser ou
Mas olha só, como o ponto cumpre as mesmas condições que usamos para encontrar o ponto , ele também pode assumir essas coordenadas. Mas sabemos que a segunda coordenada do ponto deve ser positiva. Então
Olha só! Achamos os dois de uma vez só! Hahahaha
Passo 5
Agora que sabemos que , podemos encontrar mais um vetor diretor do plano :
Ebaaa! Então o plano passa pelo ponto e tem vetores diretores e
Agora já podemos encontrar a sua equação no formato geral:
Onde é o vetor normal do plano
O vetor normal pode ser dado pelo produto vetorial entre os vetores diretores:
Então:
Então a equação do plano tem esse formato:
Como o plano passa pelo ponto , temos
Portanto, essa é a equação geral do plano :
Passo 6
Agora precisamos encontrar quem é o ponto do plano que está mais próximo do ponto
Esse ponto vai ser a intersecção do plano com a reta , onde é uma reta que passa pelo ponto e tem vetor diretor :
Um ponto genérico dessa reta pode ser escrito assim:
Como esse ponto também deve pertencer ao plano , já que é uma intersecção, ele também vai cumprir com
Logo, o ponto de intersecção entre a reta e o plano vai ser
Portanto,
Logo:
Então a alternativa correta é a letra D 😊
Ufff, essa foi longa hahahaha
Resposta
d) 4