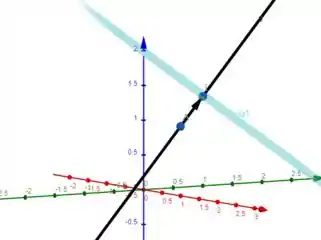
Considere os pontos
e ,
a reta de equações paramétricas
e o plano suja equação cartesiana é
Considere o ponto
d) Determine a distância do ponto ao plano e um ponto de tal que a distância entre e seja .
Passo 1
Precisamos encontrar uma reta perpendicular ao plano que contenha o ponto .
Como essa reta é perpendicular ao plano, seu vetor diretor é o vetor normal , então
Vamos chamar de o ponto de intersecção da reta com o plano . A distância entre e vai ser p módulo do vetor .
Passo 2
Primeiro vamos encontrar o ponto , intersecção de e .
Um ponto genérico de é , vamos substituir na equação de para encontrarmos o que satisfaz a intersecção:
Resolvendo essa equação, encontramos
Então vamos substituir no ponto e encontramos que nosso ponto de intersecção é
Passo 3
Sendo , temos que
A distância que procuramos, é
Passo 4
O ponto de que dista do ponto é o próprio