Calcular a distância do ponto à reta
Passo 1
Bora começar!
Para calcular a distância entre ponto e reta precisamos, primeiro, escrever um ponto genérico da reta , que será o ponto:
Passo 2
Aí, a gente lembra dessa “figurosa” e pensa: “Ahhh, agora que eu calculo o vetor ”
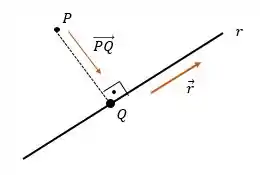
Isso aí, pequeno gafanhoto!
Sabendo o jeitão de podemos determinar o vetor :
Passo 3
Da equação da reta tiramos que e já descobrimos que
Também sabemos da teoria que o vetor diretor da reta e o vetor são ortogonais, logo:
Calculando:
Agora que achamos que podemos calcular :
Passo 4
Agora, para terminar (UFA!) vamos achar a distancia entre o ponto e a reta , é só calcular a distância entre os ponto e .
Não lembra a fórmula??
A gente relembra!
Substituindo os valores:
Resposta
Exercícios de Livros Relacionados
Seja L 1 a reta que passa pela origem e pelo ponto (1, 2, 6) e (2, 4, 8). Seja L 2 a reta de interseção dos planos π 1 e π 2 , onde π 1 é o plano x - y + 2 z + 1 = 0 e π 2 é o plano que passa pelos po
Utilize a fórmula que aparece no Exercício 39 da seção 12.4 para determinar a distância do ponto à reta dada. 1,0 , - 1 ; x = 5 - t ,y = 3 t ,z = 1 + 2 t
Obtenha os pontos da reta r que equidistam das retas s e t :a) r : x - 1 = 2 y = zs : x = y = 0 t : x - 2 = z = 0
Calcule a distância do ponto P à reta r .a) P = (0 , - 1 , 0) , r : x = 2 y - 3 = 2 z - 1
Dados o ponto A = 3,4 , - 2 e a reta x = 1 + t y = 2 - t z = 4 + 2 t Determinar o ponto simétrico de em relação à r .