Em , considere um triângulo retângulo em e isósceles (catetos de mesma medida: ) satisfazendo simultaneamente:
•
•
• A origem está no interior do triângulo.
(a) Determine as coordenadas do ponto .
(b) Determine as coordenadas do ponto .
(c) Determine a distância entre o ponto e a reta que passa por e .
(d) Determine a projeção ortogonal do ponto sobre a reta que passa por e .
Passo 1
(a) Determine as coordenadas do ponto
Bom, temos o ponto e o vetor assim podemos achar bem facinho o ponto
Passo 2
(b) Determine as coordenadas do ponto .
Temos que é perpendicular a e que ambos tem o mesmo módulo, então vamos usar isso aí:
Assim, pode ser igual a ou . Ué não poderia ser também ou ou qualquer outro vetor que favoreça a condição acima?
Nãooo!! Simplesmente pelo fato de que o módulo deve ser igual ao de então as coordenadas devem tais que a conta do módulo de a mesma. Como, sinal não importa para o módulo, temos 2 respostas possíveis.
Passo 3
Agora vamos fazer a subtração para acharmos
ou
E agora? Ficamos com essas duas respostas mesmo? Vamos dar uma olhadinha naquela informação que sobrou: a origem está no interior do triângulo. Será que essas duas respostas satisfazem isso aí?
Vamos tentar ver geometricamente:
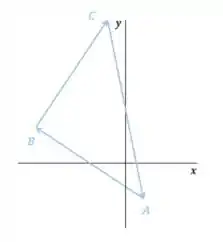
No primeiro gráfico é o ponto e a origem está dentro do triangulo e no segundo, sendo o ponto , não temos a origem dentro. Dessa forma
Passo 4
(c) Sabemos que o ângulo em é então o que precisamos é do módulo de
Isso porque para achar a distância entre um ponto e uma reta precisamos liga o ponto a reta por meio de uma reta perpendicular a essa, que no caso é a que passa por e .
Calculando o módulo...
Resposta
(d) É só lembrar que a projeção ortogonal funciona assim:
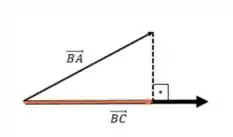
Agora, para aplicar ao caso em questão, imagina que o ângulo entre esses dois vetores é , assim como em Consegue visualizar que a projeção seria nula?
Ah, então a resposta é 0?
Nãao!! Porque aqui ele tá pedindo pra gente a projeção do ponto e não do vetor, logo, a projeção de vai ser o próprio ponto
Isso porque para achar a distância entre um ponto e uma reta precisamos ligar o ponto a reta por meio de uma reta perpendicular a essa, que no caso é a que passa por e . Dá uma olhadinha na imagem do nosso triângulo de novo pra você visualizar melhor esses paranauês.
Resposta
(a)
(b)
(c)
(d)