Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Distância entre Ponto e Reta

Ver Teoria
Exercício 6123457891011121314151617

Enunciado

Seja o triângulo A B C de vértices A = - 3 ,   1 ,   4 ,   B = - 4 ,   - 1 ,   0   e C = - 4 ,   3 ,   5 .

Calcular a medida da altura relativa ao lado B C .

Passo 1

Antes de tudo, vamos fazer um desenho para gente entender direitinho o que esse cara quer:

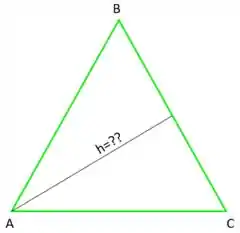
Uhh, então é esse h que o moço quer. Mas como calcula ele mesmo??

Haha, vou explicar! Reparem que o valor de h é exatamente igual ao valor da distância do ponto A à reta que passa por B e C !

Vamos começar achando a equação dessa reta!

Passo 2

Sabemos que, para achar a equação de uma reta, precisamos de um vetor diretor e de um ponto pertencente a reta. Com os pontos B e C , conseguimos calcular   B C → (que é o vetor diretor da reta)

B C → = - 4 ,   3 ,   5 - - 4 ,   - 1 ,   0

B C → = 0 ,   4 ,   5

Agora só precisamos de um ponto da reta! Vou pegar o ponto C , você poderia ter usado o B também. Com isso, a equação da nossa reta fica:

x = - 4 y = 3 + 4 t z = 5 + 5 t

Passo 3

Agora ficou um problema normal de distância entre ponto e reta!

Vamos achar o ponto genérico Q da reta:

Q = - 4 ,   3 + 4 t ,   5 + 5 t

Agora o vetor   A Q →

A Q → = - 4 ,   3 + 4 t ,   5 + 5 t - - 3 ,   1 ,   4 = ( - 1 ,   2 + 4 t ,   1 + 5 t )

Vamos achar t entonces:

A Q → ∙ B C → = 0

Calculando:

- 1 ,   2 + 4 t ,   1 + 5 t ∙ 0 ,   4 ,   5 = 8 + 16 t + 5 + 25 t = 0 → t = - 13 41

Agora que achamos que t = - 13 41 podemos calcular Q :

Q = - 4 ,   3 + 4 t ,   5 + 5 t → Q = - 4 , 71 41 ,   1 40 41

Passo 4

Último passo, galera!! Agora, para acharmos a altura h é só calcular a distância entre os pontos A = ( - 3 ,   1 ,   4 ) e Q = - 4 ,   71 41 ,   1 40 41

d P , Q = x - x 0 2 + ( y - y 0 ) 2 + ( z - z 0 ) 2

Substituindo os valores:

d A , Q = h = - 3 - ( - 4 ) 2 + 1 - 71 41 2 + 4 - 140 41 2 = 3157 41 u . c

Resposta

h = 3157 41 ≅ 1,37 u . c

Exercícios de Livros Relacionados

Seja L 1 a reta que passa pela origem e pelo ponto (1, 2, 6) e (2, 4, 8). Seja L 2 a reta de interseção dos planos π 1 e π 2 , onde π 1 é o plano x - y + 2 z + 1 = 0 e π 2 é o plano que passa pelos po
Utilize a fórmula que aparece no Exercício 39 da seção 12.4 para determinar a distância do ponto à reta dada. 1,0 , - 1 ; x = 5 - t ,y = 3 t ,z = 1 + 2 t
Obtenha os pontos da reta r que equidistam das retas s e t :a) r : x - 1 = 2 y = zs : x = y = 0 t : x - 2 = z = 0
Calcule a distância do ponto P à reta r .a) P = (0 , - 1 , 0) , r : x = 2 y - 3 = 2 z - 1
Dados o ponto A = 3,4 , - 2 e a reta x = 1 + t y = 2 - t z = 4 + 2 t Determinar o ponto simétrico de em relação à r .