UNB – Sem Campus – Física 1 – Lista – Listas de Exercício Física 1 – UnB – Lista 12 – Dinâmica do Movimento - Questão 5 – Alternativa a)
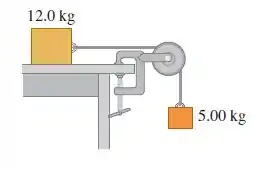
Uma caixa de em repouso sobre uma superfície horizontal e livre de atrito está atada a um peso de por um cabo delgado e leve que passa sobre uma polia com atrito desprezível (Figura abaixo). A polia possui a forma de um disco maciço e uniforme com massa de e diâmtro de . Após o sistema ser libertado, ache
a tensão no cabo sobre ambos os lados da polia
Passo 1
Eaew, tudo certinho com vocês?
Temos um problema clássico de balanço de forças ligadas por uma corda inextensível ideal com a presença de uma polia. Normalmente, nos problemas mais básicos deste tipo, a polia não causa nenhuma influência, agora, no entanto, devido as dimensões dela serem importantes, o giro da polia irá influenciar na dinâmica do sistema como um todo! Vamos começar analisando o balanço de forças e ver como isso nos ajuda a encontrar o que a alternativa nos pede! Bora lá!
Passo 2
Primeira coisa, vamos fazer o diagrama de forças deste sistema! Ele é da seguinte forma
Note que no corpo de massa , temos que apenas a força está atuando, portanto, pela segunda lei de newton, temos
No corpo de massa , temos duas forças contrárias atuando, de forma que
Note que não coloquei um índice ou , isso é porquê o sistema se move como um só, portanto, . Em um problema clássico, sem a influência da polia, teríamos que , neste caso, não podemos dizer isso, temos que . E agora, temos então variáveis para encontrar, portanto, precisamos de uma nova equação! E adivinha só! Tem tudo haver com a polia! Vem comigo!
Passo 3
Pela segunda lei de newton para a rotação, temos que
O torque resultante sofrido pela polia de momento inercia gera uma aceleração angular . Como as forças são constantes, essa aceleração também é constante, e podemos relacioná-la com a aceleração do sistema, como
E, portanto, temos que
Que torna a expressão para o torque a seguinte
Ainda precisamos relacionar isso com as nossas tensões! Mas saca só!
Passo 4
O torque realizado sobre a polia é causado pelas forças de tensão indicadas no diagrama de força, aplicadas à uma distância do eixo de giro da polia! Portanto, temos que
Ou seja, substituindo na nossa expressão para o torque resultante, temos que
Ou, isolando as tensões, temos que
Temos agora três equações, e três incógnitas! Isso já está praticamente resolvido! Bora lá!
Passo 5
Por simplicidade vou somar a equação (1) e (2), obtendo o seguinte
Qual é a vantagem disso? Nós podemos isolar , saca só! Temos que
Que acabamos de obter com a nossa equação (3). Se usarmos então a equação (3) e colocarmos alguns termos em evidência, temos que
Note que o sinal de menos aparece porquê na equação (3) temos , e aqui precisamos de ! Quase lá! Só precisamos lembrar quem é esse , você lembra? Vamo que vamo!
Passo 6
Para um disco temos que o momento de inércia é dado por
Substituindo na equação (4) temos que
Se isolarmos a aceleração, temos que
E passando os parênteses dividindo, obtemos
Agora é só substituir valores! Faz aí rapidinho! E bora para o próximo passo verificar!
Passo 7
Colocando os valores temos
Colocando na calculadora, temos aproximadamente
Vamos utilizar isso para encontrar as nossas tensões!
Passo 8
Tendo a aceleração em mãos, podemos encontrar nossas tensões como
Ou calculando os valores
E, utilizando a equação (3), temos que
De onde podemos isolar como
Substituindo os valores
Aí está a resposta desta alternativa! Te vejo na próxima! Até já!
Resposta
e