Se a superfície da figura abaixo é lisa, a aceleração do bloco será:
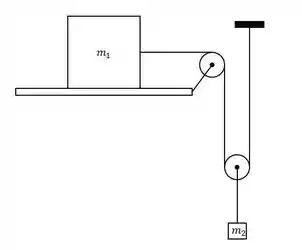
A.
B.
C.
D.
E.
Passo 1
Primeira coisa nesse tipo de problema: Não desesperar porque a figura parece complicada. Porque só parece mesmo! Hehe
Acompanha comigo que você vai ver.
Passo 2
A gente tem dois corpos ali o e o , certo?
Quando o descer, o é puxado para a direita.
Vamos fazer o diagrama de corpo livre pra cada um desses corpos. Os dois tem o peso, o tá apoiado em uma superfície, então ele tem a normal, e os dois estão sendo puxados por fios, ou seja, têm tração:
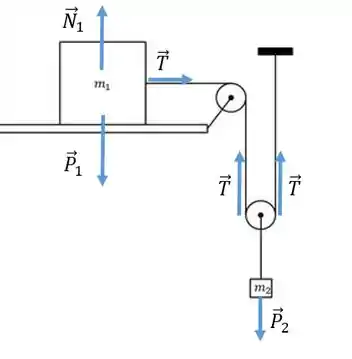
A massa tá presa pelo fio que está preso também à massa duas vezes através da polia móvel, assim sobre a massa a tração aparece duas vezes
Show!
Passo 3
Agora, vamos aplicar a segunda lei de Newton para cada um desses corpos.
Olha lá na figura, escolhi um sistema de eixos, que é positivo pra cima e pra direita, então tudo o que estiver apontando nessa direção é positivo, e se estiver na posição contrária é negativo.
Olhando para o corpo :
Mas o corpo tá se movendo na vertical? Não né. Então nessa direção :
Tá beleza, agora, na direção , nós temos movimento, então a acelereção é diferente de zero:
A única força que tá atuando nessa direção é a tração:
Maravilha!
Passo 4
Agora para o corpo 2:
Olhando lá pra figura, já marcamos o peso e a tração.
Como esse corpo tá andando pra baixo, só temos moviemento no eixo :
Vamos continuar com aquela “regrinha”, se tá apontando pro sentindo contrário ao dos eixos que eu escolhi, então é negativo!
Então o peso é negativo e a aceleração também porque o movimento é pra baixo, já a tração tá positiva:
Vamos multiplicar os dois lados por , só pra tirar aquele sinal da aceleração. (Só pra ficar bonito rs)
Show!
Passo 5
Agora, considerando que é tudo ideal, tipo a superfície é lisa, e os fios são ideais e as polias não tem massa (calma, que você não precisa se preocupar muito com isso agora...)
Olha, na prática fica bem tranquilo. Temos essas duas equações:
Passo 6
Beleza, agora com as equações montadas temos um pulo do gato! Como a massa está em uma polia móvel então o deslocamento dela será metade do deslocamento da massa , assim
Isso significa que as acelerações dessas massas obedecem
Assim, vamos resolver tudo pra que é o que ele pede! Substituindo na nossa primeira equação vamos ter
Aí você pode resolver da sua maneira favorita! O que eu vou fazer aqui vai ser multiplicar a primeira por
E agora vou somar essas duas equações
Botando o em evidência e lembrando que
Finalmente isolando
Resposta
Alternativa B.