Três blocos estão conectados entre si por roldanas e fios ideais, como mostrado no esquema da figura . Não há atrito entre as massas e as mesas e a aceleração da gravidade é .
(c) A aceleração de cada bloco e a tensão na corda se e .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu três blocos que estão conectados por fios e roldanas ideais, então a gente já pode desprezar o peso delas e o atrito, e pediu pra gente considerar e . Com isso, nós precisamos determinar as acelerações de cada bloco e a tensão no fio.
Nossa configuração é essa aqui:
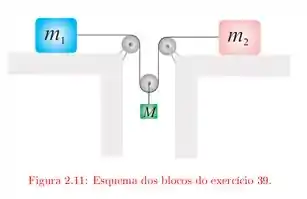
Então, vamos analisar o sistema, considerando que ele esteja em equilíbrio e considerando as forças que estão atuando em cada corpo.
Vamos lá!
Passo 2
Para calcular a aceleração de , vamos considerar as forças que estão atuando no sistema:
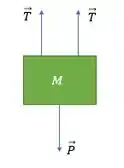
Como essas forças estão em equilíbrio, podemos dizer que:
A tração é referente as massa dos blocos e e o peso . Assim, temos:
Como e , vamos ter:
Somando:
Simplificando, temos:
Essa é a nossa aceleração .
Passo 3
No item anterior, nós vimos que e estão relacionadas através da equação:
Assim,
Substituindo do passo anterior nessa relação, temos:
Isolando e usando e , vamos ter:
Passo 4
A aceleração do bloco vai ser calculada também usando a relação , do item (b). Assim, substituindo e , vamos ter:
Passo 5
Por fim, vamos verificar o valor da tensão no fio, usando o bloco pra simplificar os cálculos. Repare que a única força horizontal atuando nele é a tensão , assim, podemos escrever:
Como e , vamos ter:
Valeu, galera! Até a próxima! 😉