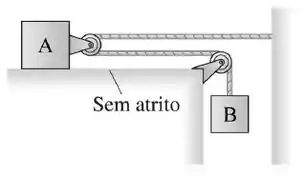
Um bloco de madeira A de massa escorrega sem atrito sobre a superfície da mesa quando puxada por uma corda sem massa onde há um corpo B pendurado de massa , como mostrado na figura. Qual é a aceleração do bloco A que desliza sobre a mesa?
(A)
(B)
(C)
(D)
(E)
Passo 1
Esse é um caso clássico de polias móveis.
Nesse exemplo, a polia do bloco A é móvel e se move junto com ele.
A diferença dessa polia para uma polia fixa, é que ela permite que a força de tração da corda atue duas vezes para o mesmo sentido:
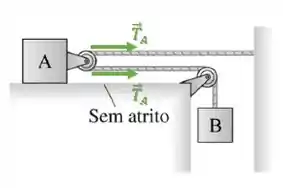
Ou seja, o bloco A é puxado com o dobro da força de tração da corda.
Em compensação, o deslocamento do bloco A cai pela metade, ou seja, o bloco A se desloca uma distância igual à metade da distância que o bloco B se desloca:
Logo, a sua aceleração também é a metade da aceleração do bloco B:
Passo 2
Para descobrir a aceleração de A, vamos fazer o Diagrama do Corpo Livre para os dois blocos e aplicar a Segunda Lei de Newton.
Bloco A:
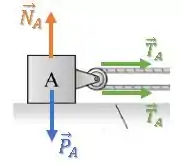
Na vertical temos um equilíbrio de forças, enquanto na horizontal, temos:
Bloco B:

A aceleração do bloco B é para baixo, logo:
A força peso é massa vezes a gravidade:
Então, temos um sistema assim:
Mas como o cabo é ideal, a tração sobre ele é a mesma em todos os pontos:
Além disso, sabemos uma relação entre as acelerações:
Logo, ficamos com esse sistema aqui:
Passo 3
Agora, basta resolver esse sistema para achar .
Como não sabemos , vamos substituir exatamente essa variável da primeira equação na segunda para que a gente elimine essa incógnita:
Substituindo isso, ficamos com:
Isolando e botando em evidância a aceleração:
Substituindo os valores:
Resposta
Letra (A)