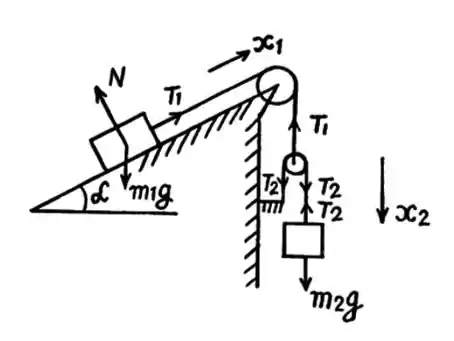
Considere o sistema com plano inclinado envolvendo polias esquematizado na figura abaixo. Não considere atrito. Assuma também que a massa das polias e dos fios são desprezíveis em comparação às massas e dos blocos e , respectivamente. Além disso, os fios não se esticam ou se deformam em geral. Note que a polia que sustenta o bloco está conectada ao fio ligado ao bloco e, assim, essa polia não está fixa.
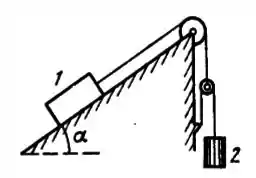
Esboce o diagrama das forças envolvidas, escreva a relação entre as diferentes tensões nos fios, e expresse a Segunda Lei de Newton para cada caso.
Demonstre a relação entre a aceleração do bloco e a aceleração do bloco .
Encontre o valor do ângulo no qual muda de sinal.
Obtenha a expressão geral para
Calcule o valor nos limites: e .
Passo 1
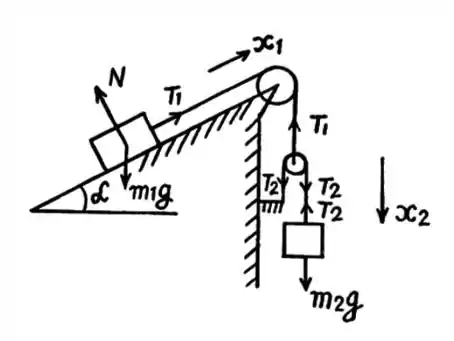
Como assumimos que a massa da polia pequena é nula, a força resultante sobre ela é nula e assim ela dividirá igualmente a força entre os dois fios. Portanto, vemos que .
As forças resultantes em cada corpo são:
Passo 2
Bom, vamos imaginar que o corpo suba uma distância , sendo . Como os fios estão conectados e sempre esticados, o corpo descerá uma distância , sendo .
Muito bem, agora é importante ter bastante atenção e imaginação ao observar a figura. Como os fios estão conectados e esticados, quando o corpo subir uma distância , a polia menor obrigatoriamente descerá uma distância .
Quando a polia menor descer uma distância , o corpo descerá uma distância , visto que seu ponto de apoio é a polia menor, se seu ponto de apoio descer, você desce junto. Mas, o fio apoiado na parte esquerda da polia menor não poderá descer essa distância , justamente por estar preso em um suporte. O que acontecerá então? Bem, a distância que o lado esquerdo do fio não desceu será transferido ao lado direito! Girando a polia menor e jogando mais fio do lado direito. Dessa forma, em vez de descer uma distância , o corpo descerá uma distância .
Logo, temos finalmente que:
Passo 3
A aceleração muda de sinal quando passa pelo zero. Assim, fazemos nas equações do item :
Agora a segunda equação:
Lembrando que , Logo:
Igualando essas expressões encontramos:
Passo 4
Usando que e , manipulamos as expressões para as forças resultantes para mostrar diretamente que:
Substituindo na segunda equação:
Ficando com o sistema:
Multiplicando a segunda equação por :
Somando as equações ficamos com:
Dividindo o numerador e denominador por , ficamos com:
Passo 5
Utilizando a expressão do item anterior, vamos começar com que é o mais fácil:
Agora para analisar , precisamos fazer isso aparecer na expressão. Então vamos multiplicar o numerador e denominador por :
Logo:
Resposta