Na figura abaixo tem-se uma massa que está conectada a uma massa através das polias e que tem massas despreziveis. Supondo que a massa desliza sobre a mesa sem atrito e que a aceleração da massa é vertical e para baixo, pede-se:
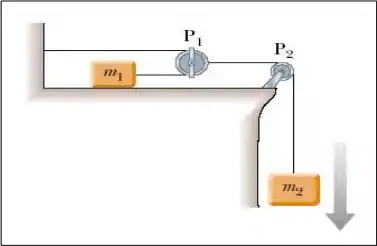
(a) Coloque em um diagrama todas as forças que atuam no sistema.
(b) Determinar o valor numérico da razão , considerando os fios inextensíveis.
(c) Determinar as trações e em função de , e .
(d) Determinar as acelerações e .
Passo 1
a)
As forças que atuam no sistema estão representadas na figura abaixo, onde corresponde a força de apoio da polia que anula a resultante das forças que atuam nessa polia e geram uma resultante no sentido oposto de .
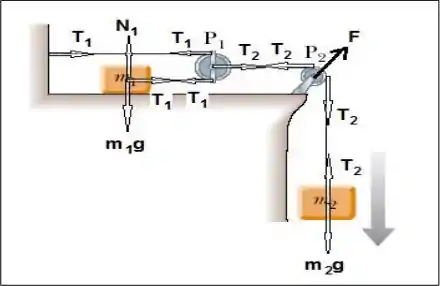
Passo 2
b)
Devido a polia não fixa que liga o bloco de massa ser conectada por 3 fios, quando a massa se deslocar de um comprimento a massa se deslocará de um comprimento . Portanto, como o bloco terá que percorrer o dobro da distância no mesmo tempo, a aceleração dele terá que ser o dobro. Então, , logo:
Passo 3
c)
Vamos primeiramente escrever as equações de movimentos para os três corpos que possuem aceleração diferente de zero que são as massas e e a polia .
Devido a massa das polias serem desprezíveis, da equação vamos ter:
Substituindo isso na equação obtemos:
Substituindo a aceleração que encontramos no item :
Da equação temos que:
Substituindo isso:
Logo vale:
E vale 2 vezes o , ou seja:
Passo 4
d)
Basta utilizar a equação do item anterior e substituir o valor da tração:
E
Resposta
a)
b)
c)
d)