USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 39a
Três blocos estão conectados entre si por roldanas e fios ideais, como mostrado no esquema da figura . Não há atrito entre as massas e as mesas e a aceleração da gravidade é .
(a) Considere , ou seja, que as massas e são iguais. Determine:
i) A razão entre as acelerações das massas e ;
ii) A aceleração de ;
iii) A tensão no fio.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu nos deu três blocos que estão conectados por fios e roldanas ideais, então a gente já pode desprezar o peso delas e o atrito, e pediu pra gente considerar que essas massas são iguais. Com isso, nós precisamos determinar a relação das acelerações dos blocos, a aceleração do bloco , que tá suspenso, e a tensão no fio, que tá “segurando” ele.
Nossa configuração é essa aqui:
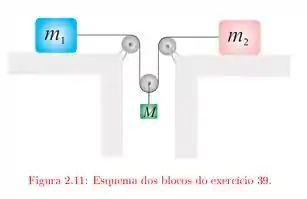
Então, vamos analisar o sistema, considerando que ele esteja em equilíbrio e considerando as forças que estão atuando em cada corpo.
Vamos lá!
Passo 2
Como os blocos se movimentam juntos e possuem massas iguais, , podemos considerar como a aceleração do sistema. Dessa forma, a aceleração entre eles vai ser sempre igual e teremos, em módulo:
Esse foi o primeiro caso.
Passo 3
Agora para calcular a aceleração de , vamos considerar as forças que estão atuando no sistema:
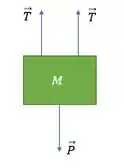
A gente tem a tração dos dois fios que estão presos ao bloco e a força peso atuando. Assim, usando a segunda lei de Newton (), vamos ter:
Como a tração é ligada aos dois blocos que possuem massas iguais, vamos ter . A força peso vai ser dada por , onde é a massa do bloco que nós estamos analisando e a constante gravitacional. Assim, temos:
Isolando :
Passo 4
Agora, para saber o valor da tensão no fio, vamos usar a mesma equação de equilíbrio do bloco :
Só que agora vamos isolar :
Mas, nós descobrimos no passo anterior que , então substituindo temos:
Aplicando a propriedade distributiva:
Tirando o M.M.C.:
Simplificando, temos:
Valeu, galera! Até a próxima! 😉