UnB, Física I, Lista 12, questão 5c
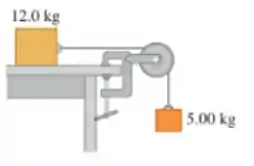
Uma caixa de em repouso sobre uma superfície horizontal e livre de atrito está atada a um peso de por um cabo delgado e leve que passa sobre uma polia com atrito desprezível (Figura abaixo). A polia possui a forma de um disco maciço e uniforme com massa de e diâmetro de . Após o sistema ser libertado, ache
c) os componentes horizontal e vertical da força que o eixo exerce sobre a polia.
Passo 1
Falaaaa, galeraaaa! Como estão? Para encontrar as componentes horizontal e vertical da força exercida pelo eixo precisamos esboçar o diagrama de corpo livre dos objetos e aplicar a segunda lei de Newton.
Passo 2
Primeiramente, esboçando o diagrama de corpo livre, obtemos:
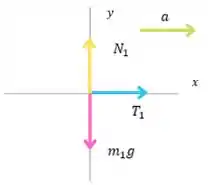
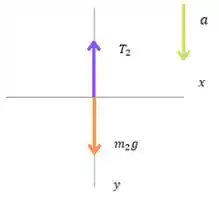
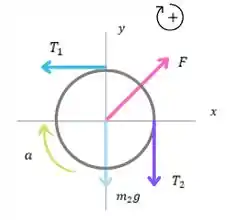
A aceleração da caixa está relacionada a aceleração da polia . Observe que e são as tensões no fio aplicadas nos dois lados da polia. Além disso, é a força exercida pelo eixo sobre a polia.
Passo 3
Aplicando a segunda lei de Newton para a primeira caixa, temos:
No eixo :
E para a segunda caixa, temos, no eixo :
Passo 4
Sabemos que o momento de inércia é dado por:
Aplicando a segunda lei na polia, temos:
Sendo nossa expressão passa a ser
Passo 5
A aceleração será calculando então somando as expressões, vamos relembrar do item a), belê?
Isolando :
Substituindo valores:
Passo 6
Podemos então obter o valor da tensão , que será:
Obtendo a tensão , temos:
Passo 7
Aplicando a segunda lei na polia, temos que no eixo :
E no eixo :
Prontinho!
