USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte I -Cinemática, Leis de Newton, Trabalho e Energia, Questão 39b
Três blocos estão conectados entre si por roldanas e fios ideais, como mostrado no esquema na figura . Não há atrito entre as massas e as mesas e a aceleração da gravidade é .
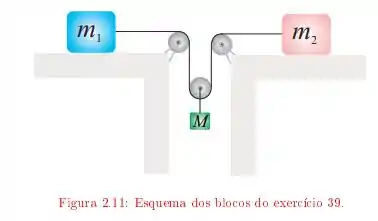
Suponha agora que as massas sejam todas diferentes. Determine
A relação entre as acelerações das massas , e ;
A aceleração de ;
A tensão no fio.
Passo 1
Oiie, tudo bem?
Temos o seguinte esquema
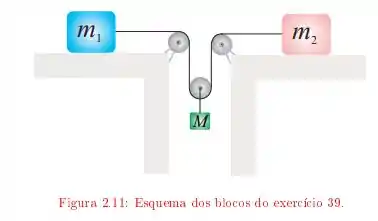
Nesta situação temos que as três massas são diferentes, e tendo isso em vista precisamos determinar
A relação entre as acelerações das massas , e ;
A aceleração de ;
A tensão no fio.
Para encontrar estas grandezas vamos estudar o seguinte diagrama de forças
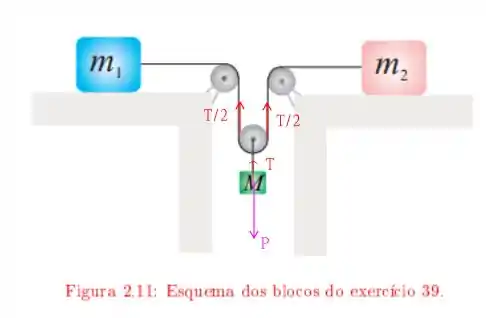
E, usar a segunda lei de Newton! Então… Bora lá!
Passo 2
O corpo de massa obedece a seguinte equação
para os outros corpos de forma que
e
dividindo uma equação pela outra temos então a relação entre as acelerações como
ou simplesmente
Agora, para obter a relação entre a aceleração do corpo de massa vamos tentar lembrar um pouco da teoria das polias móveis!
Passo 3
Uma polia móvel reduz a força necessária para se mover por a cada polia móvel aplicada, e portanto, esta polia reduz a aceleração do bloco pela metade. Tendo em vista que a aceleração do sistema acima da polia é uma resultante entre ambos os corpos, temos que
Com isso podemos encontrar as acelerações explicitamente! Note que
temos também que
portanto
como temos que
podemos escrever
usando a relação temos que
ou isolando a aceleração
novamente da relação obtemos que
e, finalmente usando a relação
Vamos achar as tensões agora!
Passo 4
Tendo as acelerações as tensões podem ser obtidas de maneira mais direta! Note que
ou simplesmente
A questão foi isso! Te vejo na próxima! Tchau Tchau!