UFRJ, Sem Campus, Física 1, Listas de F1 - Engenharias UFRJ Macaé - 3ª Lista - Dinâmica - Leis de Newton, Questão 2
No sistema da figura , e e as massas das polias e das cordas são desprezíveis. Calcule as acelerações e das massas e e a tensão na corda.
Passo 1
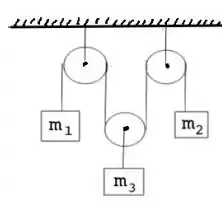
Eaee!!! Belezinha? Bom... a questão nos dá o seguinte sistema de blocos suspensos, através de cordas, pelas polias:
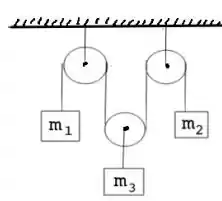
Nesse sentido, temos que calcular as acelerações e das massas e e a tensão na corda.
Para isso, podemos perceber que a quantidade de cabos é a mesma para todo o momento do nosso sistema. Dessa forma, temos:
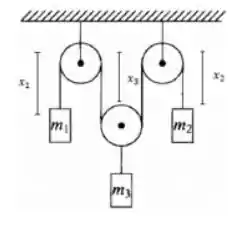
Onde .
Sendo uma constante qualquer.
Dessa forma, em conjunto com o diagrama de forças, podemos aplicar a derivada segunda para descobrirmos a aceleração do sistema!!
E aí? Bora lá?
😉
Passo 2
Então... aplicando a derivada segunda na equação do Passo 1, temos:
Já para o diagrama de corpo livre do sistema, temos:
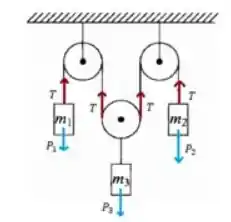
Aplicando a 2ª Lei de Newton, temos:
- Corpo 1:
- Corpo 2:
- Corpo 3:
- :
- :
- :
Passo 3
Assim, supondo que o sentido de aceleração dos corpos seja para cima (se a suposição estiver incorreta o resultado será negativo, então pode ficar tranquilo hehe), temos:
Nesse sentido, temos o seguinte sistema:
Substituindo as acelerações das três primeiras equações na quarta, temos:
Passo 4
Assim, substituindo no sistema, encontramos as acelerações:
Entendeu direitinho? Responde aee ;)
