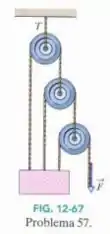
A força da Fig. 12-67 mantém o bloco de e as polias em equilíbrio. As polias têm massa e atrito desprezíveis. Calcule a tensão do cabo de cima.
Passo 1
Já aprendemos que:
- A tensão se mantém a mesma no mesmo fio
- Quando o fio dá meia volta em uma polia móvel, essa sofre o dobro da força aplicada em uma de suas extremidades.
Nesse exercício, iremos fazer o diagrama de corpo livre de cada polia e depois aplicar a primeira lei de Newton, já que foi dito que o sistema está em repouso.
Passo 2
Começando da polia mais de baixo, que vamos chamar de Polia 1.
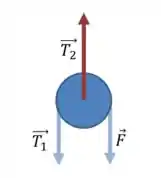
Sabemos que a tensão no fio que envolve essa polia tem que ser a mesma nas duas extremidades, portanto:
E então, como a resultante das forças é nula, temos:
O processo então se repete para a polia do meio, a Polia 2.
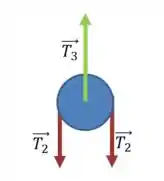
E finalmente, para a Polia 3:
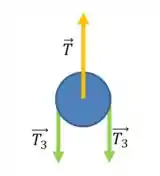
Reunindo as 3 equações obtemos:
Passo 3
Temos que arrumar um jeito agora de descobrir o valor de . Qual informação não usamos ainda? Isso mesmo! Ainda não usamos o fato de que os 3 cabos seguram uma massa dada. Vamos fazer o diagrama do bloco suspenso.
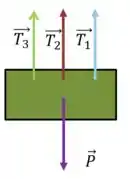
E como o bloco está em repouso:
Substituindo os valores obtidos no Passo 2 e o valor do peso do bloco, temos:
E obtemos então o valor de :
Passo 4
Agora, juntando a relação de com , encontrada no Passo 2, e com o valor de , encontrado no Passo 3, temos: