Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Transformação Linear

Ver Teoria
Exercício 331234567891011121314151617181920212223242526272829303132343536373839404142434445464748495051525354555657585960616263646566676869707172

Enunciado

USP; Sem campus; Algebra Linear 2; P2; 2022; Questão 10

Seja T   :   M 2 ( R )   →   M 2 ( R ) a transformação linear definida por T ( A )   =   A t

, para toda A   ∈   M 2 ( R ) , em que A t denota a transposta da matriz A . Assinale a alternativa

correta:

(a) T é diagonalizável e 1 é um autovalor de T com multiplicidade geométrica igual a 3

(b) T é diagonalizável e 1 é um autovalor de T com multiplicidade algébrica igual a 2

(c) T é diagonalizável e os autovalores de T são 1 e 0

(d) T não é diagonalizável e os autovalores de T são 1 e − 1

(e) T não é diagonalizável e − 1 é um autovalor de T com multiplicidade algébrica igual

a 1

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é verificar se a transformação linear T   :   M 2 ( R )   →   M 2 ( R ) definida por T ( A )   =   A t é diagonalizável.

Bem, para isso, vamos estudar o que essa transformação faz com os vetores da base

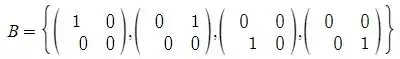
de M 2 ( R ) .

E vamos usar isso para obtermos [ T ] B . Lembrando que

[ T ] B = [ [ T ( e 1 ) ] B , [ T ( e 2 ) ] B , [ T ( e 3 ) ] B , [ T ( e 3 ) ] B ]

onde os e i ' s são os elementos da base B

Passo 2

Bem, como T ( e i ) = e i T . Logo temos que

T ( e 1 ) = e 1

= 1 e 1 + 0 e 2 + 0 e 3 + 0 e 4

⇒ [ T ( e 1 ) ] B = ( 1,0 , 0,0 )

T ( e 2 ) = e 3

= 1 e 1 + 0 e 2 + 1 e 3 + 0 e 4

⇒ [ T ( e 2 ) ] B = ( 0,0 , 1,0 )

T ( e 3 ) = e 2

= 0 e 1 + 1 e 2 + 0 e 3 + 0 e 4

⇒ [ T ( e 3 ) ] B = ( 0,1 , 0,0 )

T ( e 4 ) = e 4

= 0 e 1 + 0 e 2 + 0 e 3 + 1 e 4

⇒ [ T ( e 4 ) ] B = ( 0,0 , 0,1 )

Dessa forma, a nossa matriz [ T ] B é:

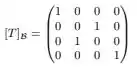
Passo 3

Agora, vamos verificar se a transformação é diagonalizável.

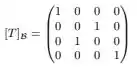
Vamos começar calculando o polinômio característico.

p ( t ) = d e t ( [ T ] B - t I )

= ( 1 - t ) 3 ( 1 + t )

Então, temos os seguintes autovalores.

1 ,   c o m   m u l t i p l i c i d a d e   a l g é b r i c a   i g u a l   a   3

- 1

Para verificarmos se T é diagonalizável, precisamos verificar a dimensão do auto espaço associado ao autovalor 1 . Nós precisamos que

d i m ( k e r ( T - 1 I ) ) = 3

Bem, vamos calcular T - 1 I

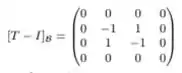
Note que a segunda linha é a terceira linha multiplicada por - 1 . Logo o nosso sistema homogêneo

[ T - 1 I ] B v = 0

terá três variáveis livres. Isso quer dizer que

d i m ( k e r ( T - 1 I ) ) = 3

Ou seja, chegamos a conclusão que T é diagonalizável.

Logo, a alternativa correta é a a )

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

a )

Exercícios de Livros Relacionados

Uma transformação linear T:R ²→R ² ² ² de posto 2 transforma toda reta numa reta. Prove isto.
De um exemplo de uma transformação linear T sobrejetiva e não injetiva. Prove que é sobrejetiva e não injetiva.
Prove que uma transformação linear é injetiva se, e somente se, seu núcleo se reduz ao único elemento 0 ∈ R 3
Prove que, para toda transformação linear M : R 3 →R 3 , a transformação M * M é auto adjunta e que o núcleo de M * M coincide com o núcleo de M . Em particular, se M é invertível, o mesmo ocorre M *
Chama-se núcleo da transformação linear M : R 3 → R 3 ao conjunto N M = { v ∈ R 3 ; M v = 0 } . Determine os núcleos das transformações lineares dos exemplos 47.1 ,47.2 ,47.3e47.4 . prove que se u , v