USP; Sem campus; Algebra Linear 2; P2; 2022; Questão 7
Seja e considere a matriz:
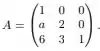
Temos que é diagonalizável se, e somente se:
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Essa é boa, pois vamos trabalhar com as condições de diagonalização.
Vamos começar dando uma revisada no conteúdo. Uma matriz é diagonalizável se os autoespaços associados aos seus autovalores tem dimensão igual à multiplicidade algébrica do autovalor. Por exemplo, se é uma matriz com dois autovalores iguais. Então devem existir dois autovetores LI associados a esse autovalor para que possa ser diagonalizável. Blz?
Com isso em mente, nosso objetivo é verificar a condição necessária para que
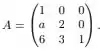
seja diagonalizável
Passo 2
Vamos começar calculando os autovalores de
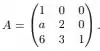
Para isso, precisamos do polinômio característico gerado por
calculando esse determinante obtemos (como a matriz é triangular o determinante é o produto dos elementos da diagonal principal):
E suas raízes são
com multiplicidade algébrica
Passo 3
Como vimos no passo , quando temos um autovalor com multiplicidade algébrica precisamos que o auto espaço associado tenha dimensão .
No nosso caso o autovalor tem multiplicidade .
Vamos calcular o auto espaço associado. Para isso precisamos resolver
onde
Logo os estão no núcleo de . Vamos calcular esse núcleo. Montando a matriz aumentada, temos:
Então, qual deve ser o valor de para que a matriz aumentada tenha duas variáveis livres?
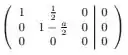
Ora, para temos duas variáveis livres, precisamos que
pois assim podemos escolher qualquer valor para e . Então
Logo, a alternativa correta é a
Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta