Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Espaços Vetoriais

Ver Teoria
Exercício 531234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515254

Enunciado

USP; Sem campus; Algebra Linear 2; P2; 2022; Questão 8

Sejam V um espaço vetorial de dimensão 2 e B   =   { e 1 ,   e 2 }   e   C   =   { f 1 ,   f 2 }

bases de V tais que:

f 1   =   3 e 1   −   2 e 2   e   f 2   =   − e 1   +   e 2 .

Se T   :   V   →   V   é a transformação linear tal que

então os autovalores de T são iguais a:

(a) 3   e   4

(b) 1   e   12

(c)   4   e   9

(d)   1   e   6

(e) 0   e   7

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é encontrar os autovalores da matriz T . lembram como calculamos eles? Eles são são as raízes do polinômio característico de T

O problema, é que o enunciado não nos diz quem é T a única coisa que sabemos é que

f 1   =   3 e 1   −   2 e 2   e   f 2   =   − e 1   +   e 2 .

Se T   :   V   →   V   é a transformação linear tal que

Como podemos obter T a partir dessas informações? Podemos obter [ T ] B . Lembram que ela é dada por

[ T ] B = [ I ] C B [ T ] B C

onde [ I ] C B pega os elementos da base de C e leva eles na base B . Vamos começar obtendo [ I ] C B

Passo 2

Como f 1   =   3 e 1   −   2 e 2   e   f 2   =   − e 1   +   e 2 .

[ I ] C B é dado por

[ I ] C B = ( ( f 1 ) B , ( f 2 ) B ) =

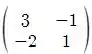
Logo temos que

[ T ] B = [ I ] C B [ T ] B C

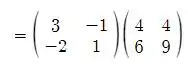
Passo 3

Por fim, vamos calcular os autovalores de

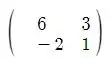
Como o polinômio característico

p ( t ) = d e t ( [ T ] B - t I )

temos que

p ( t ) = ( 6 - t ) ( 1 - t ) + 6

Usando Bhaskara, temos que as raízes desse polinômio, que são os autovalores, são:

3   e   4

Logo, a alternativa correta é a a )

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

a )

Exercícios de Livros Relacionados

Verifique se são espaços vetoriais os seguintes conjuntos:a) O R 2 com a adição usual e a multiplicação por escalar definida por α x , y = α x , 0 . b) O R 2 com x 1 , y 1 + x 2 , y 2 = ( x 1 + 2 x 2
Sejam X um conjunto não vazio e V um espaço vetorial. Mostre que, com as definições naturais de soma e multiplicação por escalar de funções, o conjunto das funções de X em V , F (X; V ), é um espaço v
Nos exercícios 5-6, em cada parte esboce, com ponto incial na origem, o vetor determinado pelos dois pontos dados.6 (a) P1(-1,0,2), P2(0,-1,0)
34 Seja P o ponto 1 ,3 ,7 . Se o ponto 4 ,0 ,- 6 for o ponto médio do segmento de reta que liga P e Q, quem é Q?
O problema apresenta um conjunto com as operações de adição e multiplicação por escalar nele definida. Verificar se é um espaço vetorial, e se não for, cite os axiomas que não se verificam. A = 0 a b