Considere as seguintes afirmações:
(I) se é uma matriz real quadrada é diagonalizável e se existe um inteiro positivo tal que , então ;
(II) se é a transformação linear definida por
para todo e se , em que , então ;
(III) se é a transformação linear definida por para todo , então é diagonalizável.
Assinale a alternativa correta:
(a) apenas as afirmações (I) e (II) são verdadeiras
(b) todas as afirmações são verdadeiras
(c) apenas as afirmações (I) e (III) são verdadeiras
(d) apenas a afirmação (I) é verdadeira
(e) apenas a afirmação (III) é verdadeira
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é verificar quais das afirmações são verdadeiras. Vamos nessa.

Vamo começar pela primeira afirmação:
se é uma matriz real quadrada é diagonalizável e se existe um inteiro positivo tal que , então ;
Bem, se é diagonalizável, então podemos escrever como
Logo,
Bem, se então
Mas isso só ocorre se . E como é a matriz DIAGONAL contendo os autovalores da matriz . Então se
já que elevar uma matriz diagonal a potência é igual a elevar cada elemento de sua diagonal principal a potência.
E se então
Logo a afirmação é verdadeira.

Passo 2
Vamos para a segunda afirmação. se é a transformação linear definida por para todo e se , em que , então ;
Vamos calcular . Como
Temos que
Então,
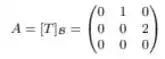
Calculando obtemos que
Portanto a segunda afirmação é verdadeira
Passo 3
Por fim, vamos para a terceira afirmativa. Se é a transformação linear definida por para todo , então é diagonalizável.
Como vimos na afirmação , para a base temos que . Mas usando o resultado da letra se for diagonalizável, e se existir um tal que , então .
Mas vimos na afirmação anterior que . Logo a terceira afirmação é falsa
portanto, a alternativa correta é a

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta