Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Transformação Linear

Ver Teoria
Exercício 711234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697072

Enunciado

USP; Sem campus; Algebra Linear 2; P2; 2022; Questão 6

Considere as seguintes afirmações:

(I) se   T   :   M 3 ( R )   →   M 2 ( R ) é uma transformação linear sobrejetora, então

d i m ( K e r ( T ) ) = 5 ;

(II) a função T   :   R 3   →   R definida por

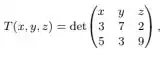
é linear

(III) Se V ́e um espaço vetorial de dimensão finita e T   :   V   →   V ́é uma transformação linear, então

  V   =   K e r ( T )   +   I m ( T ) .

Assinale a alternativa correta:

(a) apenas as afirmações (I) e (II) são verdadeiras

(b) todas as afirmações são verdadeiras

(c) apenas as afirmações (I) e (III) são verdadeiras

(d) apenas a afirmação (I) é verdadeira

(e) apenas a afirmação (III) é verdadeira

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é verificar quais das afirmações são verdadeiras. Vamos nessa.

Vamo começar pela primeira afirmação:

Se   T   :   M 3 ( R )   →   M 2 ( R ) é uma transformação linear sobrejetora, então

d i m ( K e r ( T ) ) = 5 ;

E aí? Como podemos resolver? Isso tem cara de teorema do núcleo e da imagem. Lembram dele? Ele diz que se T : V → W transformação linear, então

d i m ( V ) = d i m ( k e r ( T ) ) + d i m ( I m ( T ) )

Então, qual seria a dimensão de M 3 ( R )   e   M 2 ( R ) ?

Ora,as matrizes 3 x 3 tem nove entradas ao todo. Logo podemos construir uma base com nove matrizes, onde cada uma vale 1 em apenas uma das entradas. E, de forma análoga, M 2 ( R ) tem uma base com 4 elementos.

Logo

d i m ( M 3 ( R ) ) = 9   e   d i m ( M 2 ( R ) ) = 4

Além disso, sabemos que   T   :   M 3 ( R )   →   M 2 ( R ) é sobrejetora, isso quer dizer que sua imagem é o próprio   M 2 ( R ) . Dessa forma, podemos concluir que

  d i m ( i m ( T ) ) = 4

E pelo, teorema do núcleo e da imagem temos:

d i m ( V ) = d i m ( k e r ( T ) ) + d i m ( I m ( T ) )

⇒ 9 = d i m ( k e r ( T ) ) + 4

Logo

d i m ( K e r ( T ) ) = 5 ;

Portanto a primeira afirmação é verdadeira

Passo 2

Vamos para a segunda afirmação. A função T   :   R 3   →   R definida por

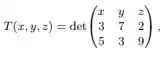
é linear

Bem, vale lembrar que o determinante é um operador linear nas colunas e nas linhas de uma matriz, isto é. Se uma linha (ou coluna) pode ser decomposta como L 1 + L 1 ' então o determinante será a soma dos determinantes das matrizes onde colocamos L 1 em uma das matrizes e L 1 ' na outra. Em equação fica assim.

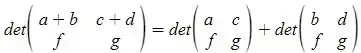
Logo, pela linearidade do determinante. T é linear. Então essa afirmativa é verdadeira

Passo 3

Por fim, vamos para a terceira afirmativa. Se V ́e um espaço vetorial de dimensão finita e T   :   V   →   V ́é uma transformaç��o linear, então

  V   =   K e r ( T )   +   I m ( T ) .

E aí, é verdade? Isso parece um teorema do núcleo e da imagem, né? Parece até verdade. Mas vamos tentar dar um contra exemplo. Vamos fazer uma transformação bem simples. Seja T : R 2 → R 2 , tal que

T ( 1,0 ) = ( 0,0 )

T ( 0,1 ) = ( 1,0 )

Logo

k e r ( T ) = I m g ( T ) = ( 1,0 )

Mas

  K e r ( T )   +   I m ( T ) = s p a n { ( 1,0 ) }

que claramente não é o R 2 . Portanto, essa afirmação é falsa.

Logo, a alternativa correta é a a )

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

a )

Exercícios de Livros Relacionados

Uma transformação linear T:R ²→R ² ² ² de posto 2 transforma toda reta numa reta. Prove isto.
De um exemplo de uma transformação linear T sobrejetiva e não injetiva. Prove que é sobrejetiva e não injetiva.
Prove que uma transformação linear é injetiva se, e somente se, seu núcleo se reduz ao único elemento 0 ∈ R 3
Prove que, para toda transformação linear M : R 3 →R 3 , a transformação M * M é auto adjunta e que o núcleo de M * M coincide com o núcleo de M . Em particular, se M é invertível, o mesmo ocorre M *
Chama-se núcleo da transformação linear M : R 3 → R 3 ao conjunto N M = { v ∈ R 3 ; M v = 0 } . Determine os núcleos das transformações lineares dos exemplos 47.1 ,47.2 ,47.3e47.4 . prove que se u , v