Seja a transformação linear tal que
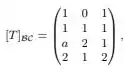
em que denota a base canônica de e denota a base canônica de .Temos que é injetora se, e somente se:
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Dessa vez vamos trabalhar com a injetividade de uma função. Mas primeiro, vamos analisar a transformação , onde sabemos que
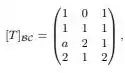
Mas vish, não temos temos apenas a matriz de transformação de base. E agora? Agradece, pois a transformação está operando sobre a base canônica, logo a nossa é a nossa matriz . Bacana, né?

Tendo isso em mente, nosso objetivo é verificar as condiçõe para ser injetora. Ou seja, não queremos que vetores distintos sejam levados em um mesmo vetor. Isso implica que vetores são levados em vetores
Passo 2
Como vimos no passo 1, a nossa é dada por
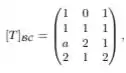
Vamos ver o que essa transformação faz com os vetores da base canônica de
Como nosso objetivo é verificar a condição para essa transformação ser injetiva, vimos que isso seria equivalente a mostrar que vetores são levados em vetores . Como os vetores da base canônica são , precisamos que
Sejam, . Mas, note que se , temos que
Ou seja, os vetores seriam . Portando
Valor presente na alternativa

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta