P3 de Álgebra Linear da UFRJ - 2016.2

Considere o produto interno usual de . Calcule a projeção ortogonal do vetor no plano

Considere o produto interno usual de e sejam e . Calcule a distância de a .

Seja o vetor da reta gerada por que é o mais próximo do vetor . Então a soma de suas entradas, , vale:

Seja . Indique a alternativa VERDADEIRA

O complemento ortogonal do núcleo de é

O complemento ortogonal do espaço gerado pelas linhas de é

O complemento ortogonal do espaço gerado pelas colunas de é

O complemento ortogonal do núcleo de é

Seja uma reflexão do através do eixo seguida da expansão de um fator na direção do eixo . Os autovalores de são:

e

e

e

e

é a matriz de uma reflexão ortogonal. O autoespaço associado ao autovalor positivo é:

A reta na direção do vetor

A reta na direção do vetor

Em um espaço vetorial munido de um produto interno, considere as seguintes afirmações:

Qualquer conjunto ortogonal de vetores não nulos é linearmente independentes.

Dados dois vetores não nulos e quaisquer, temos .

Qual das opções abaixo é CORRETA?

A afirmativa é verdadeira e é verdadeira.

A afirmativa é falsa e é falsa.

A afirmativa é verdadeira e é falsa.

A afirmativa é falsa e é verdadeira.

Considere o produto interno definido por . Determine a somadas entradas da projeção ortogonal do vetor na direção do vetor .

Considere a matriz , onde os asteriscos detotam valores quaisquer. Se a imagem de é o plano , então o valor de é:

Seja a reta que melhor ajusta os dados da tabela abaixo, no sentido dos mínimos quadrados.

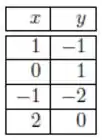
Então o coeficiente vale:

Seja um subespaço de . A dimensão de é igual a:

Considere as seguintes afirmações:

Seja uma matriz. Então a soma da dimensão da imagem de com a dimensão do núcleo da transposta de é igual a .

Se é uma matriz cujas colunas formam um conjunto ortogonal, então é uma matriz quadrada diagonal.

A alternativa é verdadeira e é verdadeira.

A alternativa é verdadeira e é falsa.

A alternativa é falsa e é falsa.

A alternativa é falsa e é verdadeira.

Note que, se é a matriz formada pelas colunas ,, então o produto tam entrada dada por

onde denota o produto interno usual.

Seja a matriz formada pelas colunas , , , onde é um conjunto ortonormal. Pode-se afirmar que:

é invertível

A imagem de é igual ao núcleo de

Seja uma base ortonormal do subespaço e seja , . Considere o vetor

(Aqui, denota o produto interno de e )

Pode-se afirmar que:

, onde denota a projeção ortogonal sobre .

é um conjunto ortogonal (mas não necessariamente ortonormal).

e são ortogonais.

.

Sejam e . Use o fato de que é uma solução no sentido dos mínimos quadrados de para calcular , a projeção ortogonal de sobre o espaço-coluna de .