A3 T14
Seja a reta que melhor ajusta os dados da tabela abaixo, no sentido dos mínimos quadrados.
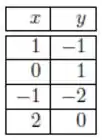
Então o coeficiente vale:
Passo 1
Só aplicarmos a fórmula dos mínimos quadrados! Vamos montar nosso sistema:
Agora passando isso para matrizes:
Pra aplicarmos mínimos quadrados agora é só multiplicarmos pela transposta nos dois lados:
Escalonando a matriz aumentada:
Resposta
Letra
Exercícios de Livros Relacionados
1. Sejam u = (1,2 , - 1) , v = (3,1 , 0) e w = (0,0 , 2) em R^3 . Calcular:a) 〈u , u〉 ; b) 〈u , w〉 ; c) 〈u , v + w〉 ; d) 〈u , u〉 ; e) ‖u + v‖^2 ; f) ‖u - v‖^2 .
1. Sejam u = (1,2 , - 1) , v = (3,1 , 0) e w = (0,0 , 2) em R^3 . Calcular:a) 〈u , u〉 ; b) 〈u , w〉 ; c) 〈u , v + w〉 ; d) 〈u , u〉 ; e) ‖u + v‖^2 ; f) ‖u - v‖^2 .
1. Sejam u = (1,2 , - 1) , v = (3,1 , 0) e w = (0,0 , 2) em R^3 . Calcular:a) 〈u , u〉 ; b) 〈u , w〉 ; c) 〈u , v + w〉 ; d) 〈u , u〉 ; e) ‖u + v‖^2 ; f) ‖u - v‖^2 .
6. Calcular a projeção do vetor x , y , z ∈ R 3 sobre o sub-espaço gerado por 1,0 , 0 e 0,1 , 0 . Fazer uma figura.
9. Pelos exercícios 7 e 8 a função u↦ p r o j g u é uma transformação linear de R n em R n . Quais são seu núcleo o e sua imagem?