P4 de Álgebra Linear da UFRJ - 2018.1

Seja S o plano gerado por e . A projeção ortogonal de sobre S vale:

(a)

(b)

(c)

(d)

Sejam , , , e . Se , então vale:

(a) 5

(b) 4

(c) 2

(d) 1

Considere o sistema abaixo:

Classifique em verdadeira ou falsa as afirmativas:

(I) O conjunto dos pontos (x,y) de que satisfazem as equações de S é uma reta de .

(II) O conjunto dos pontos (x,y,z) de que satisfazem as equações de S é uma reta de

(a) I é falsa e II é falsa.

(b) I é verdadeira e II é verdadeira.

(c) I é falsa e II é verdadeira.

(d) I é verdadeira e II é falsa.

Seja A uma matriz . Pode-se afirmar que os produtos abaixo estão bem definidos, à exceção de:

(a)

(b)

(c)

(d)

Seja A uma matriz quadrada e considere o sistema Ax=b.

I – Se ele tem solução, então

II – Se ele não tem solução, então

(a) I é falsa e II é verdadeira.

(b) I é verdadeira e II é falsa.

(c) Ambas são falsas.

(d) Ambas são verdadeiras.

Considere a forma quadrática:

Pode-se afirmar que:

(a) para todo

(b) Existem u, v tais que e

(c) para todo

(d)

Considere dois vetores não nulos de representados pelas matrizes-coluna u e v, e seja .

I –

II –

(a) I é falsa e II é falsa.

(b) I é falsa e II é verdadeira.

(c) I é verdadeira e II é falsa.

(d) I é verdadeira e II é verdadeira.

Considere o paralelepípedo em abaixo:

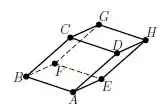
Onde e O volume deste paralelepípedo é:

(a) 15

(b) 16

(c) 17

(d) 18

Durante 50 dias, as temperaturas ao meio dia nas capitais de 100 países foram medidas e armazenadas numa matriz A. Essa é uma matriz , cujas entradas correspondem a temperatura na cidade i no dia j. Assinale a afirmativa correta:

(a) É altamente provável que uma coluna de A seja combinação linear das demais.

(b) É altamente improvável que uma coluna de A seja combinação linear das demais.

(c) Uma das colunas de A tem que ser combinação linear das demais.

(d) Nenhuma das colunas de A pode ser combinação linear das demais.

Seja A uma matriz quadrada. Considere as seguintes afirmações:

(i) Se A possui uma base ortogonal de autovetores, então A é simétrica.

(ii) Se A é simétrica, então A possui uma base ortogonal de autovetores.

(a) Ambas as afirmações são verdadeiras.

(b) Ambas as afirmações são falsas.

(c) A afirmação (i) é verdadeira e a afirmação (ii) é falsa.

(d) A afirmação (i) é falsa e a afirmação (ii) é verdadeira.

Considere um sistema linear com m equações em n incógnitas. Pode-se afirmar que:

(a) Se , a solução, se existir, será única.

(b) Se , a solução, se existir, não será única.

(c) Se , a solução, se existir, será única.

(d) Se , a solução, se existir, não será única.

Considere os vetores , e e a matriz

Onde cada representa um escalar qualquer. (Observação: dois ’s podem representar valores distintos.)

I – Se é LI, então as colunas de A são LI.

II – Se é LD, então as colunas de A são LD.

(a) I é falsa e II é falsa.

(b) I é falsa e II é verdadeira.

(c) I é verdadeira e II é verdadeira.

(d) I é verdadeira e II é falsa.

Qual dos vetores abaixo forma o maior ângulo com o vetor (1,2,0,2)?

(a) (1,-3,0,2)

(b) (1,1,-3,1)

(c) (1,2,-3,3)

(d) (1,1,1,1)

Considere as afirmativas abaixo:

I – A equação não possui solução.

I – A equação não possui solução.

(a) Ambas são falsas.

(b) Ambas são verdadeiras.

(c) I é verdadeira e II é falsa.

(d) I é falsa e II é verdadeira.

Seja Calcule

(a)

(b)

(c)

(d)

(I) A matriz cujo polinômio característico é , é diagonalizável.

(II) Se uma matriz tem polinômio característico , então é diagonalizável.

(a) (I) e (II) são falsas.

(b) (I) e (II) são verdadeiras.

(c) (I) é falsa e (II) é verdadeira.

(d) (I) é verdadeira e (II) é falsa.