P1 de Cálculo 2 da UFRJ - 2017.1

Seja a curva parametrizada por

O ponto na curva onde o vetor tangente é também um vetor normal ao plano

É:

Qual dos seguintes planos é perpendicular, simultaneamente, aos planos

E

E contém o ponto ?

Qual o ponto da curva , parametrizada por

No qual a reta tangente a contém o ponto ?

O comprimendo da curva dada pela interseção do cilindro

Com o plano

É:

Um objeto se desloca segundo o vetor posição

Se é o primeiro instante em que é ortogonal ao vetor , a velocidade escalar do objeto em é:

Seja a curva que é interseção das 2 superficies de equações

E

Então uma parametrização de , para é:

Considere a curva , descrita pelo ponto , para , como na figura:

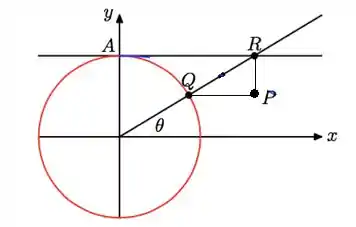
Onde o raio da circunferência é 1.

Uma parametrização de é:

5. Nenhuma das demais alternativas.

Uma função se diz limitada se existem uma constante tal que para todo o . Qual o valor de tal que a equação diferencial

Não tenha soluções limitadas?

Se é a solução do problema de valor inicial

Então é errado afirmar que

2. é limitada
3. é decrescente
4. para todo

Seja a solução do problema de valor inicial

Quanto vale ?

Se

,

Então é igual a

A solução geral de pode ser escrita na forma , onde é a solução da equação homogênena associada e É da forma:

Um tanque inicialmente contém de água pura. No instante, é introduzida no tanque água salgada com uma concentração de a uma velocidade de , e a mistura homogênea sai do tanque a uma velocidade de . Se é a quatidade em , de sal no tanque após minutos, quanto vale ?

3. Este limite não existe