Listas de Exercícios Física 1 - UnB de Física 1 da UnB - Lista 11 - Rotação de Corpos

A velocidade angular de um volante obedece à equação , onde está em segundos e e são constantes, com valores numéricos de e .

a) Quais são as unidades de e de , se está em ? b) Calcule a aceleração angular do volante para . c) Qual é o ângulo em que o volante gira durante os primeiros ?

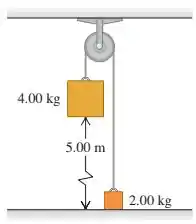
Uma polia indicada na figura abaixo possui raio e momento de inércia de . A corda não desliza sobre a periferia da polia. Use métodos de conservação da energia para calcular a velocidade do bloco de no momento em que ele atinge o solo.

As lâminas de um ventilador giram com velocidade angular dada por , onde e . a) Calcule a aceleração angular em função do tempo. b) Calcule a aceleração angular instantânea , para e a aceleração angular média, , para o intervalo de até . Como essas duas grandezas podem ser comparadas? Caso elas sejam diferentes, por que são diferentes?

Uma lâmina rotatória de um misturador gira com aceleração angular constante igual a

a) Partindo do repouso, quanto tempo ela leva para atingir uma velocidade angular de ?

Uma lâmina rotatória de um misturador gira com aceleração angular constante igual a .

b) Qual o número de revoluções descritas pela rotação da lâmina nesse intervalo de tempo?

Para , a roda de um esmeril possui velocidade angular igual a . Ela possui uma aceleração angular constante igual a , quando um freio é acionado em . A partir desse instante ela gira à medida que para com uma aceleração angular constante.

a) Qual foi o deslocamento angular total da roda desde até o instante em que ela parou?

Para , a roda de um esmeril possui velocidade angular igual a . Ela possui uma aceleração angular constante igual a , quando um freio é acionado em . A partir desse instante ela gira à medida que para com uma aceleração angular constante.

b) Em que instante ela parou?

Para , a roda de um esmeril possui velocidade angular igual a . Ela possui uma aceleração angular constante igual a , quando um freio é acionado em . A partir desse instante ela gira à medida que para com uma aceleração angular constante.

c) Qual foi o módulo da sua aceleração quando ela diminuía de velocidade?

Um volante de raio igual a parte do repouso e se acelera com aceleração angular constante

de . Calcule o módulo da aceleração tangencial, da aceleração radial e da aceleração resultante de um ponto da periferia do volante

a) no início;

Um volante de raio igual a parte do repouso e se acelera com aceleração angular constante

de . Calcule o módulo da aceleração tangencial, da aceleração radial e da aceleração resultante de um ponto da periferia do volante

b) depois de ele ter girado um ângulo de ;

Um volante de raio igual a parte do repouso e se acelera com aceleração angular constante

de . Calcule o módulo da aceleração tangencial, da aceleração radial e da aceleração resultante de um ponto da periferia do volante

c) depois de ele ter girado um ângulo de .

Quatro pequenas esferas, todas consideradas massas puntiformes com massa de , estão dispostas nos vértices de um quadrado de lado igual a e conectadas por hastes leves (figura abaixo). Calcule o momento de inércia do sistema em relação a um eixo:

a) perpendicular ao quadrado e passando pelo seu centro (um eixo passando pelo ponto 0 na figura);

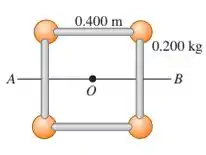
Quatro pequenas esferas, todas consideradas massas puntiformes com massa de , estão dispostas nos vértices de um quadrado de lado igual a e conectadas por hastes leves (figura abaixo). Calcule o momento de inércia do sistema em relação a um eixo:

b) cortando ao meio dois lados opostos do quadrado (um eixo ao longo da linha AB indicada na figura);

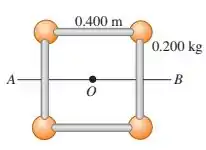
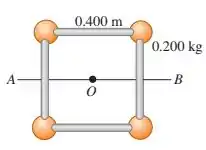
Quatro pequenas esferas, todas consideradas massas puntiformes com massa de , estão dispostas nos vértices de um quadrado de lado igual a e conectadas por hastes leves (figura abaixo). Calcule o momento de inércia do sistema em relação a um eixo:

c) passando pelo centro da esfera superior da esquerda e pelo centro da esfera inferior da direita e através do ponto 0.

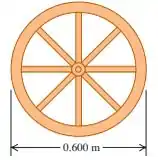
Uma roda de carroça é feita como indicado na figura abaixo. O raio da roda é igual a e possui massa igual a . Cada um dos seus oito aros, distribuídos ao longo de diâmetros, possuem comprimento de e massa igual a . Qual é o momento de inércia da roda em relação a um eixo perpendicular ao plano da roda e passando pelo seu centro?

Uma placa metálica fina de massa tem forma retangular com lados e . Use o teorema dos elementos paralelos para determinar seu momento de inércia em relação a um eixo perpendicular ao plano da placa passando por um dos seus vértices.

Engenheiros projetam um sistema por meio do qual uma massa em queda livre imprime energia cinética a um tambor uniforme em rotação, ao qual a massa está presa por um cabo delgado e leve, enrolado em volta do tambor (figura abaixo). Não há nenhum atrito significativo no eixo do tambor e tudo parte do repouso. Esse sistema está sendo testado na Terra, mas é para ser usado em Marte, onde a aceleração da gravidade é . Nos testes na Terra, quando m possui e deve cair por , ela fornece de energia cinética ao tambor.

a) Quando o sistema for operado em Marte, qual a distância a massa de terá que cair para gerar o mesmo valor de energia cinética para o tambor?

Engenheiros projetam um sistema por meio do qual uma massa em queda livre imprime energia cinética a um tambor uniforme em rotação, ao qual a massa está presa por um cabo delgado e leve, enrolado em volta do tambor (figura abaixo). Não há nenhum atrito significativo no eixo do tambor e tudo parte do repouso. Esse sistema está sendo testado na Terra, mas é para ser usado em Marte, onde a aceleração da gravidade é . Nos testes na Terra, quando m possui e deve cair por , ela fornece de energia cinética ao tambor.

b) Qual a velocidade da massa de em Marte quando o tambor obtiver de energia cinética?